
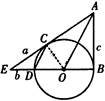
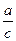 =
=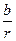 ,得r=
,得r=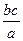
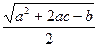
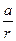 =
=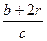 ,得r=
,得r=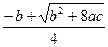 …………………8分
…………………8分 =(b+r)2,得r=
=(b+r)2,得r=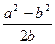
 BC,由△DCE∽△CBE,得r=
BC,由△DCE∽△CBE,得r=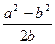
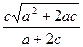 …………………8分
…………………8分

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源:不详 题型:解答题
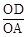 的值。
的值。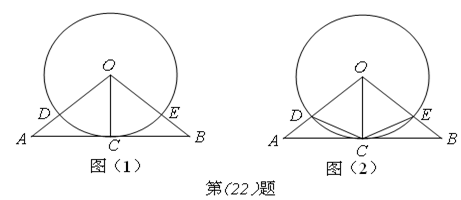
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
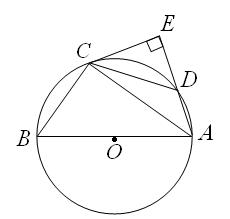
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
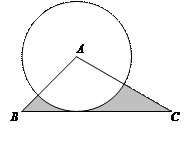
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
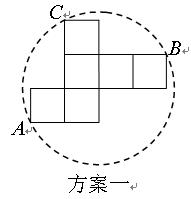
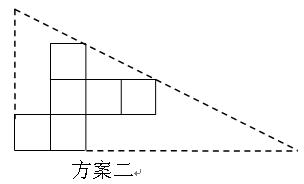

 纸片利用率=
纸片利用率= ×100%
×100% 你认为小明的这个发现是否正确,请说明理由.
你认为小明的这个发现是否正确,请说明理由.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com