
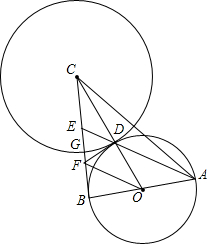
 如图:Rt△ABC中,∠ABC=90°,AB=BC,以AB为直径的⊙O交OC于D,AD的延长线交BC于E,过点D作⊙O的切线DF交BC于F,连接OF.⊙C切⊙O于点D,交BC于G
如图:Rt△ABC中,∠ABC=90°,AB=BC,以AB为直径的⊙O交OC于D,AD的延长线交BC于E,过点D作⊙O的切线DF交BC于F,连接OF.⊙C切⊙O于点D,交BC于G分析 (1)易证RT△OFD≌RT△OFB(HL),由全等三角形的性质可得∠FOD=∠FOB,又因为OA=OD,所以∠OAD=∠ODA,再由∠BOD=∠OAD+∠ODA=2∠OAD,可得∠FOB=∠OAD,进而可证明OF∥AE;
(2)点G为线段BC的一个黄金分割点,设⊙O的半径为R,则BC=AB=2R,利用勾股定理可求出OC的长,进而可求出CG的长,再计算CG和BC的比值即可;
(3)连接BD交OF于H,易证AB2=AE•AD,BE2=DE•AE,再由三角形性质可得DF:CD=OB:BC=1:2,进而可求出DF,BE的值,由DE:AD=BE2:AB2计算即可.
解答 (1)证明:
∵DF为⊙O的切线,
∴OD⊥DF,
∴∠FDO=90°
又∵∠ABC=90°,OD=OB,OF=OF,
∴在RT△OFD和RT△OFB中,
$\left\{\begin{array}{l}{OD=OB}\\{OF=OF}\end{array}\right.$,
∴RT△OFD≌RT△OFB(HL),
∴∠FOD=∠FOB,
∵OA=OD,
∴∠OAD=∠ODA,
又∵∠BOD=∠OAD+∠ODA=2∠OAD,
∴∠FOB=∠OAD,
∴OF∥AE.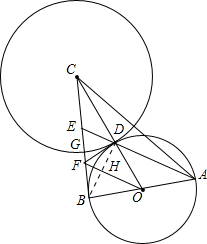
解:(2)点G为线段BC的一个黄金分割点,理由如下:
设⊙O的半径为R,则BC=AB=2R,
OC=$\sqrt{O{B}^{2}+B{C}^{2}}$=$\sqrt{5}$R,
∴CG=CD=$\sqrt{5}$R-R=($\sqrt{5}$-1)R,
∴$\frac{CG}{CB}$=$\frac{\sqrt{5}-1}{2}$,
∴G是BC的黄金分割点.
(3)连接BD交OF于H,
∵AB是直径,
∴BD⊥AE,
∴∠BDE=90°,
∵∠BAD=∠EAB,
∴△ABD∽△ABE,
∴AB2=AE•AD,
同理可证△BDE∽△ABE,
∴BE2=DE•AE,
∵∠FCD=∠OCB,∠CDF=∠CBO=90°,
∴△CDF∽△CBO,
∴DF:CD=OB:BC=1:2,
∴DF=$\frac{1}{2}$CD=$\frac{\sqrt{5}-1}{2}$R,
∵BC是⊙O的切线,
∴DF=BF,
∴DF是△BDE的中线,
∴BE=2DF=($\sqrt{5}$-1)R,
∴DE:AD=BE2:AB2=$\frac{3-\sqrt{5}}{2}$.
点评 本题考查了和圆有关的综合题目,用到的知识点有全等三角形的判定和性质、相似三角形的判定和性质、切线的性质、平行线的判定和性质以及等腰三角形的性质,题目的综合性较强,难度较大,对学生的解题能力要求很高,是一道不错的中考压轴题.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:选择题
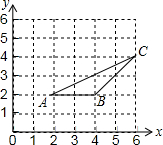 如图,△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原点0为位似中心,将△ABC缩小,使变换后得到的△DEF与△ABC对应边的比为1:2,则线段AC的中点P变换后对应的点的坐标为( )
如图,△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原点0为位似中心,将△ABC缩小,使变换后得到的△DEF与△ABC对应边的比为1:2,则线段AC的中点P变换后对应的点的坐标为( )| A. | (2,$\frac{3}{2}$) | B. | (-2,-$\frac{3}{2}$) | C. | (2,$\frac{3}{2}$)或(-2,-$\frac{3}{2}$) | D. | (8,6)或(-8,-6) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
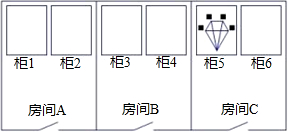 如图,有三间房,每间房内放有两个柜子,仅有一件宝物藏在某个柜子中,寻宝游戏规则如下:只允许进入三个房间中的一个房间并打开其中一个柜子即为一次游戏结束.找到宝物为游戏胜出,否则为游戏失败.
如图,有三间房,每间房内放有两个柜子,仅有一件宝物藏在某个柜子中,寻宝游戏规则如下:只允许进入三个房间中的一个房间并打开其中一个柜子即为一次游戏结束.找到宝物为游戏胜出,否则为游戏失败.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{10}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4πcm2 | B. | 9πcm2 | C. | 16πcm2 | D. | πcm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com