
����Ŀ��ijˮ���̵���5Ԫ/ǧ�˵ļ۸�һ��ˮ���������ۣ����������������5%�����������0.7Ԫ/ǧ�ˣ����費����������
��1���̵�Ҫ��ˮ���������ٶ���Ϊ����Ԫ�Ų��������
��2�������۹����У��̵귢��ÿ����֦��������m��ǧ�ˣ������۵���x��Ԫ/ǧ�ˣ�֮�������ϵm����10x+120����ô�����۵��۶�Ϊ����ʱ��ÿ���õ�����w���
��3�����̵����ÿ����һǧ��ˮ���;���aԪ����a��1����ϣ�����̣�ͨ�����ۼ�¼���֣�����۸����ÿǧ��11Ԫʱ���۳�������ÿ���������x�������С��ֱ��д��a��ȡֵ��Χ��
���𰸡���1��ˮ����Ҫ��ˮ���ۼ����ٶ�Ϊ6Ԫ/ǧ�˲Ų����������2�������۵��۶�Ϊ9Ԫ/ǧ��ʱ��ÿ��ɻ�����w���3��1��a��4
��������
��1���蹺��ˮ��kǧ��,ˮ���ۼ۶�ΪyԪ/ǧ��ʱ,ˮ����Ҫ������,�����⽨������ʽ�����ֵ�Ϳ����ˣ�
��2���ɣ�1����֪,ÿǧ��ˮ����ƽ���ɱ�Ϊ6Ԫ,�ٸ����ۼ�-����=����Ϳ��Ա�ʾ��w,Ȼ��Ϊ����ʽ�Ϳ��������ֵ��
��3�����������г��۳������������ΪP��x�ĺ�����ϵ,�õ��Գ��᷽��,�����ۼ۸����ÿǧ��11Ԫʱ,�۳�������ÿ�������P��x�������С�õ�����a�IJ���ʽ,,��֮�ɵã�
�⣺��1���蹺��ˮ��kǧ��,ˮ���ۼ۶�ΪyԪ/ǧ��ʱ,ˮ���̲Ų������,�������
yk��1��5%������5+0.7��k,
��k��0�ɽ�ã�y��6,
����,ˮ����Ҫ��ˮ���ۼ����ٶ�Ϊ6Ԫ/ǧ�˲Ų��������
��2���ɣ�1����֪,ÿǧ��ˮ����ƽ���ɱ�Ϊ6Ԫ,�������
w����x��6����m
����x��6������10x+120��
����10��x��9��2+90
���,��x��9ʱ,w�����ֵ��
����,�����۵��۶�Ϊ9Ԫ/ǧ��ʱ,ÿ��ɻ�����w���
��3����۳������������ΪP,
��P����x��6��a������10x+120������10x2+��10a+180��x��120��a+6��,
�����߿�������,�Գ���Ϊֱ��x��![]() ,
,
�����ۼ۸����ÿǧ��11Ԫʱ,�۳�������ÿ�������P��x�������С,
��![]() ��11,��ã�a��4,
��11,��ã�a��4,
��1��a��4��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ŀڴ������ĸ���ȫ��ͬ��С�����Ƿֱ���Ϊ![]() ��
��![]() ��
��![]() ��
��![]() �������ȡһ��С��Ȼ��Żأ��������ȡһ����
�������ȡһ��С��Ȼ��Żأ��������ȡһ����
���û���״ͼ���б��ķ������������¼��ĸ��ʣ�
��1������ȡ����С������ͬ��
��2������ȡ����С���ŵĺ͵���4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
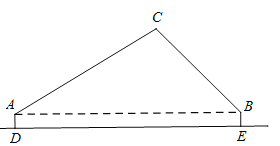
����Ŀ��ij��ѧС���ڽ����ˮƽ�յ��϶����˻����в��ʵ�飮��ͼ����̨����Ƿֱ����A��Bλ�ã��������߾�Ϊ1�ף���![]() �ף�����̨��������50�ף���AB=50�ף�����ijһʱ�����˻�λ�ڵ�C (��C���A��B��ͬһƽ���ڣ���A�����������Ϊ
�ף�����̨��������50�ף���AB=50�ף�����ijһʱ�����˻�λ�ڵ�C (��C���A��B��ͬһƽ���ڣ���A�����������Ϊ![]() ��B�����������Ϊ
��B�����������Ϊ![]() �����ο����ݣ�
�����ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��1�����ʱ�����˻�����ظ߶ȣ�����λ���ף��������������
��2�����˻���ˮƽ�����������2����F����F���A��B��C��ͬһƽ���ڣ�����ʱ��A��������˻�������Ϊ![]() �������˻�ˮƽ���е�ƽ���ٶȣ�����λ����/�룬�������������
�������˻�ˮƽ���е�ƽ���ٶȣ�����λ����/�룬�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y��2x��ֱ��x��2�ཻ�ڵ�A����������y��x2���߶�OA�ӵ�O�˶�����A��ʹ�䶥��ʼ�����߶�OA�ϣ���������ֱ��x��2�ཻ�ڵ�P�����P�ƶ���·����Ϊ��������

A.4B.3C.2D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
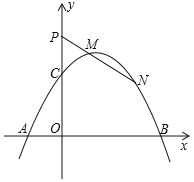
����Ŀ����֪������y��ax2��2ax+3��x�ύ�ڵ�A��B��A��B�ң�����AB��4����y�ύ��C�㣮
��1���������ߵĽ���ʽ��
��2����ͼ��֤�����������������һ��P��0��b����b��3�������ڹ���P��һ��ֱ�߽���������M��N���㣬ʹ��PM��MN������
��3��������������0��x��4��IJ��ּ�Ϊͼ��G����ͼ��G��ֱ��y��t�Ϸ��IJ�����y��t���ۣ����ಿ�ֱ��ֲ��䣬�õ�һ���µĺ�����ͼ��������������ֵΪm����СֵΪn����m��n��6����t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ŀڴ���װ�к졢�ơ���������ɫ��С�����ɸ���С�����ɫ�������ͬ�������л���2��������1�����������������һ������������ĸ�����![]() ��
��
��1����ڴ������ĸ�����
��2����һ���������һ�����Żأ����ڶ������������һ���������б�����״ͼ�ķ�������������������ǡ��һ��һ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
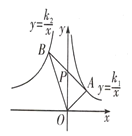
����Ŀ����ͼ����A��B�ֱ��ڷ���������y=![]() (k1��0) �� y=
(k1��0) �� y=![]() (k2��0)��ͼ���ϣ�����AB��y���ڵ�P���ҵ�A���B����P�����ĶԳ�.����AOB�����Ϊ4����k1-k2=______.
(k2��0)��ͼ���ϣ�����AB��y���ڵ�P���ҵ�A���B����P�����ĶԳ�.����AOB�����Ϊ4����k1-k2=______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У���A�İ뾶Ϊ2��Բ������Ϊ��4��0����y�����е�B��0��3������C�ǡ�A�ϵĶ��㣬��P��BC���е㣬��OP�ķ�Χ�ǣ�������

A.![]() B.2��OP��4C.
B.2��OP��4C.![]() ��OP��
��OP��![]() D.3��OP��4
D.3��OP��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������![]() ��y�ύ�ڵ�A��
��y�ύ�ڵ�A��
��1��ֱ��д����A�����ꣻ
��2����A��B���ڶԳ���Գƣ����B�����ꣻ
��3����֪��![]() ��
��![]() �������������߶�PQǡ�����������㣬��Ϻ���ͼ����a��ȡֵ��Χ��
�������������߶�PQǡ�����������㣬��Ϻ���ͼ����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com