
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆. 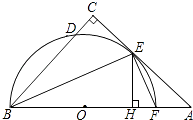
(1)求证:AC是⊙O的切线.
(2)过点E作EH⊥AB于点H,求证:CD=HF.
【答案】
(1)证明:如图1,连接OE.
∵BE⊥EF,
∴∠BEF=90°,
∴BF是圆O的直径.
∵BE平分∠ABC,
∴∠CBE=∠OBE,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠OEB=∠CBE,
∴OE∥BC,
∴∠AEO=∠C=90°,
∴AC是⊙O的切线;
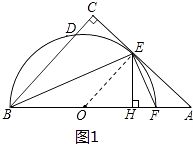
(2)证明:如图2,连结DE.
∵∠CBE=∠OBE,EC⊥BC于C,EH⊥AB于H,
∴EC=EH.
∵∠CDE+∠BDE=180°,∠HFE+∠BDE=180°,
∴∠CDE=∠HFE.
在△CDE与△HFE中,
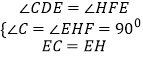 ,
,
∴△CDE≌△HFE(AAS),
∴CD=HF.
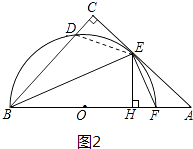
【解析】(1)连接OE,由于BE是角平分线,则有∠CBE=∠OBE;而OB=OE,就有∠OBE=∠OEB,等量代换有∠OEB=∠CBE,那么利用内错角相等,两直线平行,可得OE∥BC;又∠C=90°,所以∠AEO=90°,即AC是⊙O的切线;(2)连结DE,先根据AAS证明△CDE≌△HFE,再由全等三角形的对应边相等即可得出CD=HF.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论:①AS=AR,②QP∥AR,③△BPR≌△QPS中一定正确的是( )
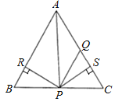
A. 全部正确 B. 仅①和②正确 C. 仅①正确 D. 仅①和③正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场经营的某品牌童装,4月的销售额为20000元,为扩大销量,5月份商场对这种童装打9折销售,结果销量增加了50件,销售额增加了7000元.
(1)求该童装4月份的销售单价;
(2)若4月份销售这种童装获利8000元,6月全月商场进行“六一儿童节”促销活动.童装在4月售价的基础上一律打8折销售,若该童装的成本不变,则销量至少为多少件,才能保证6月的利润比4月的利润至少增长25%?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 20 | 30 |
根据图标提供的信息,下列结论错误的是( )

A. 这次被调查的学生人数为200人 B. 扇形统计图中E部分扇形的圆心角为72°
C. 被调查的学生中最想选F的人数为35人 D. 被调查的学生中最想选D的有55人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上. 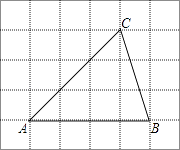
(1)△ABC的面积等于;
(2)若四边形DEFG是△ABC中所能包含的面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺画出该正方形,并简要说明画图方法(不要求证明) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句:①有一边对应相等的两个直角三角形全等;②一般三角形具有的性质,直角三角形都具有;③有两边相等的两直角三角形全等;④两直角三角形的斜边为5cm,一条直角边都为3cm,则这两个直角三角形必全等.其中正确的有________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点B的坐标是(﹣1,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.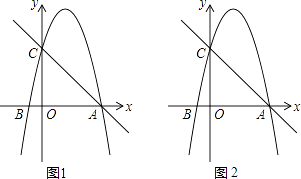
(1)求抛物线的解析式;
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,写出点P的坐标(不要求写解题过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=x2+bx﹣5的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为( )
A.x1=0,x2=4
B.x1=1,x2=5
C.x1=1,x2=﹣5
D.x1=﹣1,x2=5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com