
| A. | 90° | B. | 45° | C. | 30° | D. | 60° |
分析 画出图形,连接OP,根据对称轴是对称点连线的垂直平分线可知:OB是PP1的垂直平分线,OA是PP2的垂直平分线,由垂直平分线性质得:OP=OP1=OP2,所以根据等腰三角形三线合一得:∠P1OB=∠POB和∠P2OA=∠POA,则所求的∠P1OP2的度数是∠AOB的度数的2倍.
解答 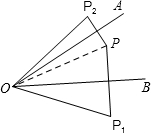 解:如图所示,连接OP,
解:如图所示,连接OP,
∵P1与P关于OB对称,
∴OB是PP1的垂直平分线,
∴OP=OP1,
∴∠P1OB=∠POB,
同理得:∠P2OA=∠POA,
∴∠POA+∠POB=∠P2OA+∠P1OB,
∴∠P2OP1=2∠AOB=2×30°=60°,
故选D.
点评 本题考查了轴对称的性质,熟练掌握如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.而垂直平分线上的点与线段两个端点的距离相等;得到等腰三角形后,要熟知等腰三角形的性质:①等边对等角,②三线合一等;使问题得对解决.


 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①④ | D. | ②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com