
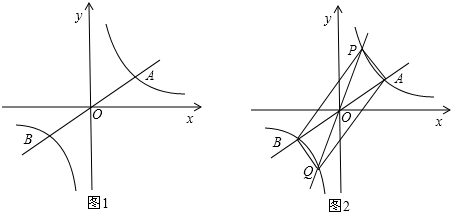
分析 (1)根据双曲线关于原点对称求出点B的坐标,结合图象得到$\frac{k}{x}$≤k′x时,x的取值范围;
(2)①根据对角线互相平分的四边形是平行四边形证明即可;
②过点A、B分别作y轴的平行线,过点P、Q分别作x轴的平行线,分别交于C、D、E、F,根据正方形的面积公式和三角形的面积公式计算即可.
解答 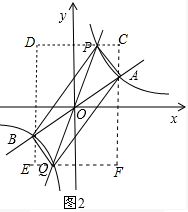 解:(1)∵双曲线y=$\frac{k}{x}$关于原点对称,点A的坐标为(3,1),
解:(1)∵双曲线y=$\frac{k}{x}$关于原点对称,点A的坐标为(3,1),
∴点B的坐标为(-3,-1),
由图象可知,当-3≤x<0或x≥3时,$\frac{k}{x}$≤k′x,
故答案为:(-3,-1);-3≤x<0或x≥3;
(2)①∵双曲线y=$\frac{k}{x}$关于原点对称,
∴OA=OB,OP=OQ,
∴四边形APBQ一定是平行四边形,
故答案为:平行四边形;
②∵点A的坐标为(3,1),
∴k=3×1=3,
∴反比例函数的解析式为y=$\frac{3}{x}$,
∵点P的横坐标为1,
∴点P的纵坐标为3,
∴点P的坐标为(1,3),
由双曲线关于原点对称可知,点Q的坐标为(-1,-3),点B的坐标为(-3,-1),
如图2,过点A、B分别作y轴的平行线,过点P、Q分别作x轴的平行线,分别交于C、D、E、F,
则四边形CDEF是矩形,
CD=6,DE=6,DB=DP=4,CP=CA=2,
则四边形APBQ的面积=矩形CDEF的面积-△ACP的面积-△PDB的面积-△BEQ的面积-△AFQ的面积
=36-2-8-2-8
=16.
点评 本题考查的是反比例函数的图形和性质、反比例函数图象上点的坐标特征、中心对称图形的概念和性质以及平行四边形的判定,掌握双曲线是关于原点的中心对称图形、平行四边形的判定定理是解题的关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:选择题
| A. | 987654321 | B. | 987654311 | C. | 987654221 | D. | 987654421 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
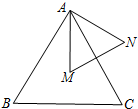 如图,△ABC和△AMN都是等边三角形,点M是△ABC的重心,那么$\frac{{S}_{△AMN}}{{S}_{△ABC}}$的值为( )
如图,△ABC和△AMN都是等边三角形,点M是△ABC的重心,那么$\frac{{S}_{△AMN}}{{S}_{△ABC}}$的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
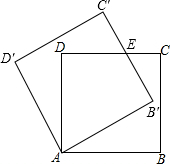 如图,边长为1的正方形ABCD绕点A逆时针旋转30°得正方形AB′C′D′,边B′C′与CD交于点E,则四边形AB′ED的面积是( )
如图,边长为1的正方形ABCD绕点A逆时针旋转30°得正方形AB′C′D′,边B′C′与CD交于点E,则四边形AB′ED的面积是( )| A. | $\frac{3}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 1805年,法军在拿破仑的率领下与德军在莱茵河畔激战.德军在莱茵河北岸Q处,如图所示,因不知河宽,法军很难瞄准敌军,聪明的拿破仑站在南岸的点O处调整好自己的帽子,使视线恰好擦着帽舌边缘看到敌军兵营Q处,然后后退到B点,这是他的视点恰好能落在0处,于是他命令部下测量他脚站的B处与0点之间的距离,并下令按这个距离炮轰敌营,法军能命中目标吗?请说明理由.
1805年,法军在拿破仑的率领下与德军在莱茵河畔激战.德军在莱茵河北岸Q处,如图所示,因不知河宽,法军很难瞄准敌军,聪明的拿破仑站在南岸的点O处调整好自己的帽子,使视线恰好擦着帽舌边缘看到敌军兵营Q处,然后后退到B点,这是他的视点恰好能落在0处,于是他命令部下测量他脚站的B处与0点之间的距离,并下令按这个距离炮轰敌营,法军能命中目标吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com