练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】二次函数y＝ax2+bx+c的图象如图所示、则下列结论：①abc＞0；②a﹣5b+9c＞0；③3a+c＜0，正确的是(　　)

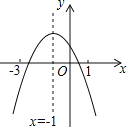
    A.①③B.①②C.①②③D.②③

    【答案】C

    【解析】

    由抛物线对称轴的位置判断ab的符号，由抛物线与y轴的交点判断c的符号，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．

    解：①∵抛物线的对称轴在y轴的左侧，

    ∴ab＞0，

    由图象可知：c＞0，

    ∴abc＞0，

    故①正确；

    ②∵ x＝﹣＝﹣1，

    ∴b＝2a，

    又∵c＞0，由开口向下得a<0,

    ∴ a﹣5b+9c＝9c﹣9a＝9（c﹣a）＞0，

    故②正确，

    ③∵b＝2a，

    由图象可知：9a﹣3b+c＜0，

    ∴9a﹣6a+c＜0，即3a+c＜0，

    故③正确；

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

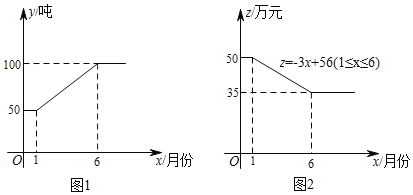
    【题目】随着技术的发展进步，某公司2018年采用的新型原料生产产品．这种新型原料的用量y（吨）与月份x之间的关系如图1所示，每吨新型原料所生产的产品的售价z（万元）与月份x之间的关系如图2所示．已知将每吨这种新型原料加工成的产品的成本为20万元．

    （1）求出该公司这种新型原料的用量y（吨）与月份x之间的函数关系式；

    （2）若该公司利用新型原料所生产的产品当月都全部销售，求哪个月利润最大，最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

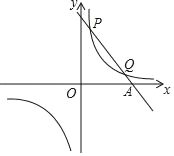
    【题目】已知一次函数y＝k1x+b与反比例函数y＝的图象交于第一象限内的P（，8），Q（4，m）两点，与x轴交于A点．

    （1）写出点P关于原点的对称点P′的坐标；

    （2）分别求出这两个函数的表达式；

    （3）求∠P′AO的正切值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是半圆O的直径，D是半圆O上一点，C是的中点，连结AC交BD于点E，连结AD，若BE＝4DE，CE＝6，则AB的长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，抛物线y＝﹣x2+bx+c与x轴交于点A（﹣3，0）和点B，与y轴交于点C （0，2）．

    （1）求抛物线的表达式，并用配方法求出顶点D的坐标；

    （2）若点E是点C关于抛物线对称轴的对称点，求tan∠CEB的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知在⊙O中，直径MN＝10，正方形ABCD的四个顶点分别在⊙O及半径OM、OP上，并且∠POM＝45°，求正方形的边长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

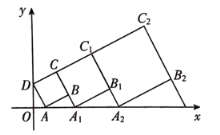
    【题目】在平面直角坐标系中，正方形ABCD 的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2），延长CB交x轴于点A1，作正方形A1CC1B1，延长C1B1交x轴于点A2，作正方形A2C1C2B2，…，按照这样的规律作正方形，则点B2019的纵坐标为_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】佛山一环高速化改造后正式收费，车辆经过平胜大桥收费站时，设置了 4 个 ETC 智能收费（即不 需要人工收费）通道，分别为 A、B、C、D 通道，车辆可随机选择其中的一个直接读卡通过．

    （1）一辆车经过此收费站时，选择 A 通道通过的概率是___________；

    （2）现有甲、乙两辆小车从同一方向通过此收费站，请你用树状图或列表格求出两辆车选择不同通道通过的概率

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+bx+2交x轴于A（﹣1，0），B（4，0）两点，交y轴于点C，与过点C且平行于x轴的直线交于另一点D，点P是抛物线上一动点．

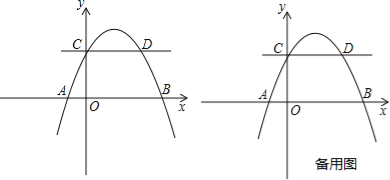
    （1）求抛物线解析式及点D坐标；

    （2）点E在x轴上，若以A，E，D，P为顶点的四边形是平行四边形，求此时点P的坐标；

    （3）过点P作直线CD的垂线，垂足为Q，若将△CPQ沿CP翻折，点Q的对应点为Q′．是否存在点P，使Q′恰好落在x轴上？若存在，求出此时点P的坐标；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案