
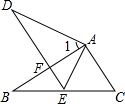
 如图,△ABC≌△ADE,∠1=70°,点E正好在线段BC上,求∠FEB和∠EAC.
如图,△ABC≌△ADE,∠1=70°,点E正好在线段BC上,求∠FEB和∠EAC. 分析 根据全等三角形对应边相等可得AC=AE,全等三角形对应角相等可得∠BAC=∠DAE,∠DEA=∠C,再求出∠EAC=∠1,然后根据等腰三角形两底角相等求出∠C,再根据平角等于180°列式计算即可求出∠FEB.
解答 解:∵△ABC≌△ADE,
∴AC=AE,∠BAC=∠DAE,∠DEA=∠C,
∴∠BAC-∠BAE=∠DAE-∠BAE,
即∠EAC=∠1,
∵∠1=70°,
∴∠EAC=70°,
又∵AE=AC,
∴∠AEC=∠C=$\frac{1}{2}$(180°-∠EAC)=$\frac{1}{2}$(180°-70°)=55°,
∴∠FEB=180°-∠DAE-∠AEC=180°-55°-55°=70°.
点评 本题考查了全等三角形的性质,等腰三角形的性质,解答时,除必备的知识外,还应将条件和所求联系起来,即将所求的角与已知角通过全等及三角形内角之间的关系联系起来.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com