
【题目】先化简,再求值: ![]() ÷(a+2﹣
÷(a+2﹣ ![]() ),其中x2﹣2
),其中x2﹣2 ![]() x+a=0有两个不相等的实数根,且a为非负整数.
x+a=0有两个不相等的实数根,且a为非负整数.
【答案】解: ![]() ÷(a+2﹣
÷(a+2﹣ ![]() ) =
) = 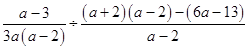
= ![]()
= ![]()
= ![]()
= ![]() ,
,
∵x2﹣2 ![]() x+a=0有两个不相等的实数根,且a为非负整数,
x+a=0有两个不相等的实数根,且a为非负整数,
∴△= ![]() 且a≥0,a为整数,
且a≥0,a为整数,
解得,0≤a<3且a为整数,
∵a﹣2≠0,a≠0,
∴a=1,
当a=1时,原式= ![]() .
.
【解析】根据分式的额加减法和除法可以化简题目中的式子,再根据x2﹣2 ![]() x+a=0有两个不相等的实数根,且a为非负整数和求得的a的值必须使得原分式有意义,从而可以求得a的值,然后代入化简后的式子即可解答本题.
x+a=0有两个不相等的实数根,且a为非负整数和求得的a的值必须使得原分式有意义,从而可以求得a的值,然后代入化简后的式子即可解答本题.
【考点精析】解答此题的关键在于理解求根公式的相关知识,掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.


科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD中,AB=6 cm,BC=8 cm,点E是BC边上一点,连接AE,并将△AEB沿AE折叠,得到△AEB′,以C,E,B′为顶点的三角形是直角三角形时,BE的长为____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN∥BC,BD⊥DC,∠1=∠2=60°.
(1)AB 与 DE 平行吗?请说明理由;
(2)若 DC 是∠NDE 的平分线.
①试说明∠ABC=∠C;
②试说明 BD 是∠ABC 的平分线.
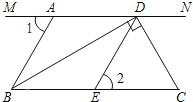
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),C(0,4)两点,与x轴交于另一点B,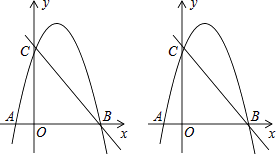
(1)求抛物线的解析式;
(2)求P在第一象限的抛物线上,P点的横坐标为t,过点P向x轴做垂线交直线BC于点Q,设线段PQ的长为m,求m与t之间的函数关系式并求出m的最大值;
(3)在(2)的条件下,抛物线上一点D的纵坐标为m的最大值,连接BD,在抛物线是否存在点E(不与点A,B,C重合)使得∠DBE=45°?若不存在.请说明理由;若存在请求E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一间阶梯教室,第1排的座位数为a,从第2排开始,每一排都比前一排增加b个座位,
(1)请你在下表的空格里填写一个适当的式子:
第1排座位数 | 第2排座位数 | 第3排座位数 | 第4排座位数 | …… |
a | a+b | a+2b` | …… |
(2)已知第4排有18个座位,第15排的座位数是第5排座位数的2倍,求第21排有多少个座位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y= ![]() 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO= ![]() ,OB=4,OE=2.
,OB=4,OE=2. 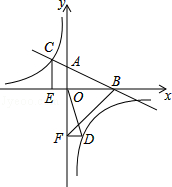
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO , 求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某广电局与长江证券公司联合推出广电宽带网业务,用户通过宽带网可以享受新闻点播、影视欣赏、股市大户室等项服务,用户缴纳上网费的方式有:方式一:每月80元包月;方式二:每月上网费y(元)与上网时间x(小时)的函数关系用如图所示的折线表示;方式三:以0小时为起点,每小时收费1.6元,月收费不超过120元.若设一用户每月上网x小时,月上网费为y元.

(1)根据图象,写出方式二中y(元)与x(小时)的函数关系式;
(2)试写出方式三中y(元)与x(小时)的函数关系式;
(3)若此用户每月上网60小时,选用哪种方式上网其费用最少?最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,P是菱形ABCD的对角线AC上一动点,过P垂直于AC的直线交菱形ABCD的边于M、N两点,设AC=2,BD=1,AP=x,则△AMN的面积为y,则y关于x的函数图象的大致形状是( )
A.
B.
C.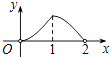
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |
请结合图表完成下列各题:
(1)①表中a的值为; ②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是 .
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com