
分析 (1)先根据平方差公式,单项式乘多项式,完全平方公式计算,再合并同类项计算即可求解;
(2)先根据完全平方公式,平方差公式计算,再合并同类项计算即可求解;
(3)先算乘方,再算乘除法,再计算加减法即可求解,注意先算括号里面的和绝对值,以及乘法分配律的灵活应用;
(4)根据平方差公式计算,再约分计算即可求解.
解答 解:(1)(a+b)(a-b)-a(a+b)-(a-b)2
=a2-b2-a2-ab-a2+2ab-b2
=-a2+ab-2b2;
(2)4(a-b)2-(2a+b)(-b+2a)
=4a2-8ab+4b2-4a2+b2
=-8ab+5b2;
(3)$-{2}^{5}÷(-4)-|-1-3|×(\frac{1}{2})^{2}+(1\frac{1}{8}+2\frac{1}{3}-3\frac{3}{4})×24$
=-32÷(-4)-4×$\frac{1}{4}$+$\frac{9}{8}$×24+$\frac{7}{3}$×24-$\frac{15}{4}$×24
=8-1+27+56-90
=0
(4)(1-$\frac{1}{2^2}$)(1-$\frac{1}{3^2}$)(1-$\frac{1}{4^2}$)…(1-$\frac{1}{{{{2014}^2}}}$)
=(1-$\frac{1}{2}$)×(1+$\frac{1}{2}$)×(1-$\frac{1}{3}$)×(1+$\frac{1}{3}$)×(1-$\frac{1}{4}$)×(1+$\frac{1}{4}$)×…×(1-$\frac{1}{2014}$)×(1+$\frac{1}{2014}$)
=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$×$\frac{3}{4}$×$\frac{5}{4}$×…×$\frac{2013}{2014}$×$\frac{2015}{2014}$
=$\frac{2015}{4028}$.
点评 考查了整式的混合运算,(1)有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相同.(2)“整体”思想在整式运算中较为常见,适时采用整体思想可使问题简单化,并且迅速地解决相关问题,此时应注意被看做整体的代数式通常要用括号括起来.同时考查了有理数的混合运算.


科目:初中数学 来源: 题型:选择题
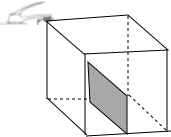 如图,在一个正方体容器底部正中央嵌入一块平行于侧面的矩形隔板,隔板的高是正方体棱长的一半,现匀速向隔板左侧注水(到容器注满时停止),设注水时间为t(min),隔板所在平面左侧的水深为y左(cm),则y左与t的函数图象大致是( )
如图,在一个正方体容器底部正中央嵌入一块平行于侧面的矩形隔板,隔板的高是正方体棱长的一半,现匀速向隔板左侧注水(到容器注满时停止),设注水时间为t(min),隔板所在平面左侧的水深为y左(cm),则y左与t的函数图象大致是( )| A. |  | B. | 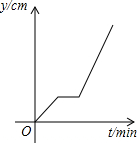 | C. | 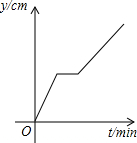 | D. | 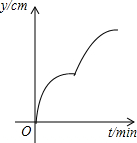 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
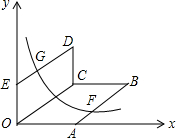 如图,0为原点,A(4,0),E(0,3),四边形OABC,四边形OCDE都为平行四边形,OC=5,函数y=$\frac{k}{x}$(x>0)的图象经过AB的中点F和DE的中点G,则k的值为9.
如图,0为原点,A(4,0),E(0,3),四边形OABC,四边形OCDE都为平行四边形,OC=5,函数y=$\frac{k}{x}$(x>0)的图象经过AB的中点F和DE的中点G,则k的值为9.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
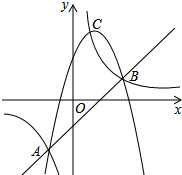 已知Y1,Y2,Y3分别表示二次函数、反比例函数和一次函数的三个函数值,它们的交点分别是A(-1,-2)、B(2,1)和C($\frac{2}{3}$,3),规定M={Y1,Y2,Y3中最小的函数值},则下列结论:
已知Y1,Y2,Y3分别表示二次函数、反比例函数和一次函数的三个函数值,它们的交点分别是A(-1,-2)、B(2,1)和C($\frac{2}{3}$,3),规定M={Y1,Y2,Y3中最小的函数值},则下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com