
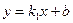 与反比例函数
与反比例函数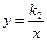 的图象交于A
的图象交于A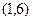 ,B
,B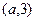 两点.
两点.
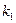 、
、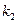 的值?
的值?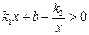 时x的取值范围?
时x的取值范围?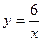
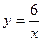 的图象上,
的图象上,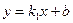 过点A
过点A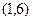 ,B(2,3)
,B(2,3)
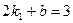 解得:k1=-3 b=9………………2分
解得:k1=-3 b=9………………2分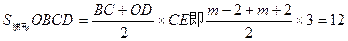
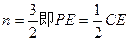 ……………………………1分
……………………………1分

科目:初中数学 来源: 题型:
(本题10分)如图,直线x-2y=-5和x+y=1分别与x轴交于A、B两点,这两条线的交点为P.
1.(1)求点P的坐标.
2.(2)求△APB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
(本题10分)如图,P是双曲线![]() 的一个分支上的一点,以点P为圆心,1个单位长度为半径作⊙P,设点P的坐标为(
的一个分支上的一点,以点P为圆心,1个单位长度为半径作⊙P,设点P的坐标为(![]() ,
,![]() ).
).
(1)求当![]() 为何值时,⊙P与直线
为何值时,⊙P与直线![]() 相切,并求点P的坐标.
相切,并求点P的坐标.
(2)直接写出当![]() 为何值时,⊙P与直线
为何值时,⊙P与直线![]() 相交、相离.
相交、相离.

查看答案和解析>>
科目:初中数学 来源: 题型:
(本题10分)如图,以点M(-1,0)为圆心的圆与y轴、x轴分别交于点A、B、C、D,直线y=- x- 与⊙M相切于点H,交x轴于点E,交y轴于点F.
1.(1)请直接写出OE、⊙M的半径r、CH的长;(3分)
2.(2)如图1,弦HQ交x轴于点P,且DP:PH=3:2,求COS∠QHC的值;(3分)
3.(3)如图2,点K为线段EC上一动点(不与E、C重合),连接BK交⊙M于点T,弦AT交x轴于点N.是否存在一个常数a,始终满足MN·MK=a,如果存在,请求出a的值;如果不存在,请说明理由.(3分)

查看答案和解析>>
科目:初中数学 来源:2011-2012学年湖北武夷山市九年级上学期期末考试数学卷.doc 题型:解答题
(本题10分)如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.
试判断直线BD与⊙O的位置关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源:2010年北京师大附中初一第一学期期末考试数学卷 题型:解答题
(本题10分)如图4,边长为 的矩形,它的周长为14,面积为10,求下列各式的值:(1)
的矩形,它的周长为14,面积为10,求下列各式的值:(1) (2)
(2) 


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com