
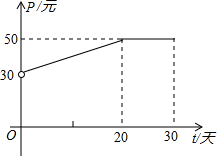
 根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.
根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.| t/天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 | 10 |
分析 (1)首先根据图象,当0<t≤20时,设该产品每件销售价格P与时间t的函数解析式为:P=at+b,然后把(0,30)、(20,50)代入,求出P与时间t的函数解析式;然后求出20<t≤30时,该产品每件销售价格P与时间t的关系即可.
(2)首先根据表中提供的数据描出实数对(t,Q)的对应点;然后设日销售量Q与时间t的一个函数解析式为Q=mt+n,把(5,35)、(15,25)代入,求出Q与时间t的函数解析式即可.
(3)首先根据题意,设日销售金额为y元,然后分两种情况:①0<t≤20;②20<t≤30;根据日销售金额=每件产品销售价格×日销售量,求出日销售金额与时间的关系式;然后分别求出0<t≤20、20<t≤30时日销售金额最大值,确定出在这30天内,哪一天的日销售金额最大即可.
解答 解:(1)当0<t≤20时,设该产品每件销售价格P与时间t的函数解析式为:P=at+b,
把(0,30)、(20,50)代入,
可得$\left\{\begin{array}{l}{30=b}\\{50=20a+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=30}\end{array}\right.$,
所以当0<t≤20时,
P=t+30;
当20<t≤30时,
P=50;
综上,可得该产品每件销售价格P与时间t的关系为:
P=$\left\{\begin{array}{l}{t+30(0<t≤20)}\\{50(20<t≤30)}\end{array}\right.$;
(2)如图,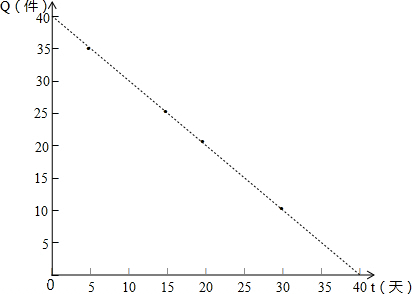 ,
,
设日销售量Q与时间t的一个函数解析式为Q=mt+n,
把(5,35)、(15,25)代入,
可得$\left\{\begin{array}{l}{35=5m+n}\\{25=15m+n}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-1}\\{n=40}\end{array}\right.$,
所以Q=-t+40,
把(20,20)、(30,10)代入Q=-t+40,销售量Q与时间t的关系式也成立,
所以日销售量Q与时间t的一个函数解析式为:
Q=-t+40(0<t≤30)
(3)设日销售金额为y元,
则y=$\left\{\begin{array}{l}{(t+30)(-t+40),(0<t≤20)}\\{50(-t+40),(20<t≤30)}\end{array}\right.$
=$\left\{\begin{array}{l}{{-t}^{2}+10t+1200,(0<t≤20)}\\{-50t+2000,(20<t≤30)}\end{array}\right.$
①当0<t≤20时,
y=-t2+10t+1200
=-(t-5)2+1225
当t=5时,ymax=1225;
②当20<t≤30时,
y=-50t+2000<-50×20+2000=1000,
因为1000<1225,
所以这30天内,第5天的日销售金额最大,是1225元.
答:在这30天内,第5天的日销售金额最大,是1225元.
点评 (1)此题主要考查了函数解析式的确定,考查了分类讨论思想的应用,注意自变量的取值范围.
(2)此题还考查了函数最值的求法,注意配方法的应用,注意函数单调性的判断,要熟练掌握.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:选择题
 点P在数轴上运动,它所对应的数值为a,如图,当点P从点A运动到点B,则代数式$\sqrt{(a-1)^{2}}$+a+3的最大值为( )
点P在数轴上运动,它所对应的数值为a,如图,当点P从点A运动到点B,则代数式$\sqrt{(a-1)^{2}}$+a+3的最大值为( )| A. | 4 | B. | a+1 | C. | 6 | D. | a+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
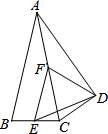 如图,△ABC中,AB=AC,以AC为斜边作Rt△ADC,使∠ADC=90°,∠CAD=∠CAB=26°,E、F分别是BC、AC的中点,则∠EDF等于51°.
如图,△ABC中,AB=AC,以AC为斜边作Rt△ADC,使∠ADC=90°,∠CAD=∠CAB=26°,E、F分别是BC、AC的中点,则∠EDF等于51°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com