
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知AB是⊙O的直径,AT与⊙O相切于点A,⊙O交BT于C,CT=CB.
如图,已知AB是⊙O的直径,AT与⊙O相切于点A,⊙O交BT于C,CT=CB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 飞行员在空中观察地面的区域是一个圆(如图),当观察角α为50°,飞机的飞行高度h为9.8×102m时,观察区域的半径为多少米(结果精确到1m)?如果观察角度不变,要使观察区域面积增加1倍,那么飞机要升高多少米(精确到1m)?
飞行员在空中观察地面的区域是一个圆(如图),当观察角α为50°,飞机的飞行高度h为9.8×102m时,观察区域的半径为多少米(结果精确到1m)?如果观察角度不变,要使观察区域面积增加1倍,那么飞机要升高多少米(精确到1m)?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
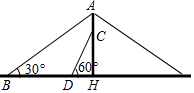 芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,在同类型重载桥梁中,它的主跨度居世界第二.如图,是该桥面上的一根立柱和拉索的示意图,小明测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索底端距离BD为20米,且已知两拉索顶端的距离AC为2米,请求出立柱AH的长.(结果精确到0.1米,$\sqrt{3}$≈1.732)
芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,在同类型重载桥梁中,它的主跨度居世界第二.如图,是该桥面上的一根立柱和拉索的示意图,小明测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索底端距离BD为20米,且已知两拉索顶端的距离AC为2米,请求出立柱AH的长.(结果精确到0.1米,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
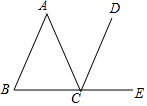 如图,在△ABC中,AB=AC,CD∥AB,点E在BC的延长线上,若∠A=30°,则∠DCE的大小为( )
如图,在△ABC中,AB=AC,CD∥AB,点E在BC的延长线上,若∠A=30°,则∠DCE的大小为( )| A. | 30° | B. | 52.5° | C. | 75° | D. | 85° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com