
【题目】阅读理(解析)
提出问题:如图1,在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间有什么关系?探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
当AP=![]() AD时(如图2):
AD时(如图2):
∵AP=![]() AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,
∴S△ABP=![]() S△ABD,
S△ABD,
∵PD=AD﹣AP=![]() AD,△CDP和△CDA的高相等
AD,△CDP和△CDA的高相等
∴S△CDP=![]() S△CDA,
S△CDA,
∴S△PBC=S四边形ABCD﹣S△ABP﹣S△CDP=S四边形ABCD﹣![]() S△ABD﹣
S△ABD﹣![]() S△CDA,
S△CDA,
=S四边形ABCD﹣![]() (S四边形ABCD﹣S△DBC)﹣
(S四边形ABCD﹣S△DBC)﹣![]() (S四边形ABCD﹣S△ABC)=
(S四边形ABCD﹣S△ABC)=![]() S△DBC+
S△DBC+![]() S△ABC.
S△ABC.
(1)当AP=![]() AD时,探求S△PBC与S△ABC和S△DBC之间的关系式并证明;
AD时,探求S△PBC与S△ABC和S△DBC之间的关系式并证明;
(2)当AP=![]() AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
(3)一般地,当AP=![]() AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系为: ;
AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系为: ;
(4)当AP=![]() AD(0≤
AD(0≤![]() ≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .
≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .

【答案】(1)S△PBC=![]() S△DBC+
S△DBC+![]() S△ABC,证明见解析;(2)S△PBC=
S△ABC,证明见解析;(2)S△PBC=![]() S△DBC+
S△DBC+![]() S△ABC;(3)S△PBC=
S△ABC;(3)S△PBC=![]() S△DBC+
S△DBC+![]() S△ABC;(4)S△PBC=
S△ABC;(4)S△PBC=![]() S△DBC+
S△DBC+![]() S△ABC.
S△ABC.
【解析】
(1)根据题中的方法进行求解即可;(2)由(1)即可得到;(3)方法同(1),进行求解;(4)利用(3)中的结论即可求解.
(1)∵AP=![]() AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,
∴S△ABP=![]() S△ABD.
S△ABD.
又∵PD=AD﹣AP=![]() AD,△CDP和△CDA的高相等,
AD,△CDP和△CDA的高相等,
∴S△CDP=![]() S△CDA.
S△CDA.
∴S△PBC=S四边形ABCD﹣S△ABP﹣S△CDP
=S四边形ABCD﹣![]() S△ABD﹣
S△ABD﹣![]() S△CDA
S△CDA
=S四边形ABCD﹣![]() (S四边形ABCD﹣S△DBC)﹣
(S四边形ABCD﹣S△DBC)﹣![]() (S四边形ABCD﹣S△ABC)
(S四边形ABCD﹣S△ABC)
=![]() S△DBC+
S△DBC+![]() S△ABC.
S△ABC.
∴S△PBC=![]() S△DBC+
S△DBC+![]() S△ABC
S△ABC
(2)由(1)得,S△PBC=![]() S△DBC+
S△DBC+![]() S△ABC;
S△ABC;
(3)S△PBC=![]() S△DBC+
S△DBC+![]() S△ABC;
S△ABC;
∵AP=![]() AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,
∴S△ABP=![]() S△ABD.
S△ABD.
又∵PD=AD﹣AP=![]() AD,△CDP和△CDA的高相等,
AD,△CDP和△CDA的高相等,
∴S△CDP=![]() S△CDA
S△CDA
∴S△PBC=S四边形ABCD﹣S△ABP﹣S△CDP
=S四边形ABCD﹣![]() S△ABD﹣
S△ABD﹣![]() S△CDA
S△CDA
=S四边形ABCD﹣![]() (S四边形ABCD﹣S△DBC)﹣
(S四边形ABCD﹣S△DBC)﹣![]() (S四边形ABCD﹣S△ABC)
(S四边形ABCD﹣S△ABC)
=![]() S△DBC+
S△DBC+![]() S△ABC.
S△ABC.
∴S△PBC=![]() S△DBC+
S△DBC+![]() S△ABC
S△ABC
(4)由(3)得,S△PBC=![]() S△DBC+
S△DBC+![]() S△ABC.
S△ABC.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,直线a∥直线b,点A、D在直线a上,点B、C在直线b上,连接AB、AC、BD、DC,得△ABC和△BDC,△ABC的面积_______△BDC的面积(填“>”、“=”或“<”).
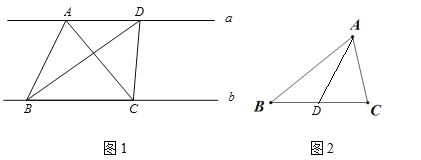

(2)如图2,已知△ABC,过点A有一条线段,将△ABC的面积平分,且交BC于点D,则![]() .
.
(3)如图3,已知四边形ABCD,请过点D作一条线段DG将四边形ABCD面积平分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC和正方形CDEF在平面直角坐标系中,点O,C,F在y轴上,点O为坐标原点,点M为OC的中点,抛物线y=ax2+b经过M,B,E三点,则 ![]() 的值为 .
的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.
(1)求抛物线的表达式;
(2)D为抛物线在第二象限部分上的一点,作DE垂直x轴于点E,交线段AM于点F,求线段DF长度的最大值,并求此时点D的坐标;
(3)抛物线上是否存在一点P,作PN垂直x轴于点N,使得以点P、A、N为顶点的三角形与△MAO相似(不包括全等)?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家蓝莓采摘园的草莓品质相同,销售价格都是每千克30元,“五一”假期,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园购买60元的门票,采摘的蓝莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘的蓝莓超过10千克后,超过部分五折优惠,优惠期间,设某游客的蓝莓采摘量为![]() (千克),在甲采摘园所需总费用为
(千克),在甲采摘园所需总费用为![]() (元),在乙采摘园所需总费用为
(元),在乙采摘园所需总费用为![]() (元).
(元).
(1)当采摘量超过10千克时,求![]() 与
与![]() 的关系式;
的关系式;
(2)若要采摘40千克蓝莓,去哪家比较合算?请计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
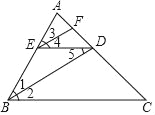
【题目】如图,BD是∠ABC的平分线,ED∥BC,∠4=∠5,则EF也是∠AED的平分线.完成下列推理过程:
证明:∵BD是∠ABC的平分线(已知)
∴∠1=∠2(角平分线定义)
∵ED∥BC(已知)
∴∠5=∠2( )
∴∠1=∠5(等量代换)
∵∠4=∠5(已知)
∴EF∥ ( )
∴∠3=∠1( )
∴∠3=∠4(等量代换)
∴EF是∠AED的平分线(角平分线定义)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn=____.(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一块直角三角板ABC中,∠C=90°,∠A=30°,BC=1,将另一个含30°角的△EDF的30°角的顶点D放在AB边上,E,F分别在AC,BC上,当点D在AB边上移动时,DE始终与AB垂直,若△CEF与△DEF相似,则AD= . 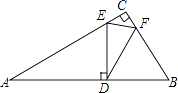
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com