
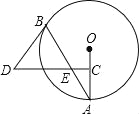
【题目】如图,AB是⊙O的弦,点C为半径OA的中点,过点C作CD⊥OA交弦AB于点E,连接BD,且DE=DB.
(1)判断BD与⊙O的位置关系,并说明理由;
(2)若CD=15,BE=10,tanA=![]() ,求⊙O的直径.
,求⊙O的直径.
【答案】(1)BD是⊙O的切线,理由见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OB,由已知条件易证∠OBD=90°,即可证明BD是⊙O的切线;(2)过点D作DG⊥BE于G,根据等腰三角形的性质得到EG=![]() BE=5,由两角相等的三角形相似,△ACE∽△DGE,利用相似三角形对应角相等得到sin∠EDG=sinA=
BE=5,由两角相等的三角形相似,△ACE∽△DGE,利用相似三角形对应角相等得到sin∠EDG=sinA=![]() ,在Rt△EDG中,利用勾股定理求出DG的长,根据三角形相似得到比例式,代入数据即可得到结果.
,在Rt△EDG中,利用勾股定理求出DG的长,根据三角形相似得到比例式,代入数据即可得到结果.
试题解析:(1)证明:连接OB,
∵OB=OA,DE=DB,
∴∠A=∠OBA,∠DEB=∠ABD,
又∵CD⊥OA,
∴∠A+∠AEC=∠A+∠DEB=90°,
∴∠OBA+∠ABD=90°,
∴OB⊥BD,
∴BD是⊙O的切线;
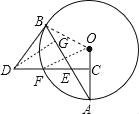
(2)如图,过点D作DG⊥BE于G,
∵DE=DB,
∴EG=![]() BE=5,
BE=5,
∵∠ACE=∠DGE=90°,∠AEC=∠GED,
∴∠GDE=∠A,
∴△ACE∽△DGE,
∴sin∠EDG=sinA=![]() =
=![]() ,即CE=13,
,即CE=13,
在Rt△ECG中,
∵DG=![]() =12,
=12,
∵CD=15,DE=13,
∴DE=2,
∵△ACE∽△DGE,
∴![]() =
=![]() ,
,
∴AC=![]() DG=
DG=![]() ,
,
∴⊙O的直径2OA=4AD=![]() .
.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】下列用代数式表示不正确的是( )
A. a、b两数的平方和表示为a2+b2; B. a、b两数的和的平方表示为(a+b)2;
C. a与b的平方的和表示为a2+b2; D. a与b的和的平方表示为(a+b)2;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】微信红包是沟通人们之间感情的一种方式,已知小明在2016年”元旦节”收到微信红包为300元,2018年为363元,若这两年小明收到的微信红包的年平均增长率为x,根据题意可列方程为( )
A. 363(1+2x)=300 B. 300(1+x2)=363
C. 300(1+x)2=363 D. 300+x2=363
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
①已知:a+![]() =1+
=1+![]() ,求a2+
,求a2+![]() 的值.
的值.
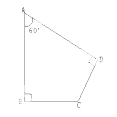
②如图,四边形ABCD中∠A=60°,∠B=∠D=90°,AB=2,CD=1,求四边形ABCD的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠B=∠C=∠EDF=α,BD=CF,BE=CD,则下列结论正确的是( )
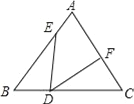
A. 2α+∠A=180° B. α+∠A=90° C. 2α+∠A=90° D. α+∠A=180°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com