
 用40cm长的绳子围成矩形ABCD,设AB=xm,矩形ABCD的面积为S(m2)
用40cm长的绳子围成矩形ABCD,设AB=xm,矩形ABCD的面积为S(m2)| x | … | 8 | 9 | 9.5 | 10 | 10.5 | 11 | 12 | … |
| S | … | 96 | 99 | 99.75 | 100 | 99,75 | 99 | 96 | … |
分析 (1)根据矩形的面积公式即可求出S.
(2)利用(1)中的函数关系式,把自变量x的值代入计算即可.
(3)观察(2)中计算结果,即可判断.
解答 解:(1)由题意S=x•$\frac{40-2x}{2}$=-x2+20x.
(2)x=8时,S=96,
x=9时,S=99,
x=9.5时,S=99.75,
x=10时,S=100,
x=10.5时,S=99.75,
x=11时,S=99,
x=12时,S=96.
故答案分别为96,99,99.75,100,99.75,99,96.
(3)猜想:x=10时,S的值最大.
点评 本题考查二次函数的应用,矩形的性质等知识,解题的关键是记住矩形的面积公式,学会构建函数关系式解决实际问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
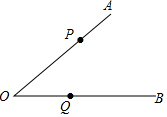 已知点P、Q分别在∠ACB的边OA、OB上,按下列要求画图
已知点P、Q分别在∠ACB的边OA、OB上,按下列要求画图查看答案和解析>>
科目:初中数学 来源: 题型:解答题
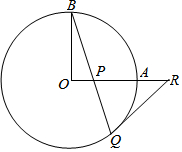 如图,OA和OB是⊙O的半径,并且OA⊥OB.P是OA上任意一点,BP的延长线交⊙O于点Q,点R在OA的延长线上,且RP=RQ.
如图,OA和OB是⊙O的半径,并且OA⊥OB.P是OA上任意一点,BP的延长线交⊙O于点Q,点R在OA的延长线上,且RP=RQ.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com