
【题目】已知:抛物线y=x2+bx+c经过点(2,-3)和(4,5)。

(1)求抛物线的表达式及顶点坐标;
(2)将抛物线沿x轴翻折,得到图象G,求图象G的表达式;
(3)在(2)的条件下,当-2<x<2时,直线y=m与该图象有一个公共点,求m的值或取值范围。
【答案】(1)y=x²-2x-3;(1,-4);(2)y=-x²+2x+3;(3)4,或-5<m≤3.
【解析】试题分析:(1)把(2,-3)和(4,5)分别代入y=x+bx+c然后解方程组即可得到抛物线的表达式,配方化为顶点式可得顶点坐标;(2)利用对称性可得图象G的表达式;(3)y=m过抛物线顶点(1,4)时,直线y=m与该图象有一个公共点,此时y=4,∴m="4." 利用图象可确定另一情况-5<m≤3.
试题解析:(1)把(2,-3)和(4,5)分别代入y=x+bx+c
得: ![]() ,解得:
,解得: ![]() ,
,
∴抛物线的表达式为:y=x-2x-3.
∵y=x-2x-3=(x-1)2-4.
∴顶点坐标为(1,-4).
(2)∵将抛物线沿x轴翻折,
得到图象G与原抛物线图形关于x轴对称,
∴图像G的表达式为:y=-x+2x+3.
(3)如图,

当0≤x<2时,y=m过抛物线顶点(1,4)时,
直线y=m与该图象有一个公共点,
此时y=4,∴m=4.
当-2<x<0时,直线y=m与该图象有一个公共点,
当y=m过抛物线上的点(0,3)时, y=3,∴m=3.
当y=m过抛物线上的点(-2,-5)时, y=-5,∴m=-5.
∴-5<m<3.
综上:m的值为4,或-5<m≤3.


科目:初中数学 来源: 题型:
【题目】如图,半径为1个单位的圆片上有一点Q与数轴上的原点重合(提示:圆的周长C=2πr,本题中π的取值为3.14)
(1)把圆片沿数轴向右滚动1周,点Q到达数轴上点A的位置,点A表示的数是;
(2)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,﹣5,+4,+3,﹣2
①第几次滚动后,Q点距离原点最近?第几次滚动后,Q点距离原点最远?
②当圆片结束运动时,Q点运动的路程共有多少?此时点Q所表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具店购进一种儿童玩具,计划每个售价36元,能盈利80%,在销售中出现了滞销,于是先后两次降价,售价降为25元.
(1)求这种玩具的进价;
(2)求平均每次降价的百分率(精确到0.1%).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在□ABCD中,AE⊥BC于E,E恰为BC的中点,tanB=2。



(1)求证:AD=AE;
(2)如图2,点P在BE上,作EF⊥DP于点F,连结AF,求证:DF-EF=![]() AF;
AF;
(3)请你在图3中画图探究:当P为射线EC上任意一点(P不与点E重合)时,作EF⊥DP于点F,连结AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论为____________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( )
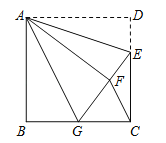
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下面的程序计算:
当输入 ![]() 时,输出结果是299;当输入
时,输出结果是299;当输入 ![]() 时,输出结果是466;如果输入
时,输出结果是466;如果输入 ![]() 的值是正整数,输出结果是257,那么满足条件的
的值是正整数,输出结果是257,那么满足条件的 ![]() 的值最多有( )
的值最多有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com