
【题目】已知:如图,点A、B分别是∠MON的边OM、ON上两点,OC平分∠MON,在∠CON的内部取一点P(点A、P、B三点不在同一直线上),连接PA、PB.
(1)探索∠APB与∠MON、∠PAO、∠PBO之间的数量关系,并证明你的结论;
(2)设∠OAP=x°,∠OBP=y°,若∠APB的平分线PQ交OC于点Q,求∠OQP的度数(用含有x、y的代数式表示).


【答案】(1)见解析;(2)∠OQP=180°+![]() x°﹣
x°﹣![]() y°或∠OQP=
y°或∠OQP=![]() x°﹣
x°﹣![]() y°.
y°.
【解析】【试题分析】(1)分下面两种情况进行说明;
①如图1,点P在直线AB的右侧,∠APB+∠MON+∠PAO+∠PBO=360°,
②如图2,点P在直线AB的左侧,∠APB=∠MON+∠PAO+∠PBO,
(2)分两种情况讨论,如图3和图4.
【试题解析】
(1)分两种情况:
①如图1,点P在直线AB的右侧,∠APB+∠MON+∠PAO+∠PBO=360°,
证明:∵四边形AOBP的内角和为(4﹣2)×180°=360°,
∴∠APB=360°﹣∠MON﹣∠PAO﹣∠PBO;

②如图2,点P在直线AB的左侧,∠APB=∠MON+∠PAO+∠PBO,
证明:延长AP交ON于点D,
∵∠ADB是△AOD的外角,
∴∠ADB=∠PAO+∠AOD,
∵∠APB是△PDB的外角,
∴∠APB=∠PDB+∠PBO,
∴∠APB=∠MON+∠PAO+∠PBO;
(2)设∠MON=2m°,∠APB=2n°,
∵OC平分∠MON,
∴∠AOC=![]() ∠MON=m°,
∠MON=m°,
∵PQ平分∠APB,
∴∠APQ=![]() ∠APB=n°,
∠APB=n°,
分两种情况:
第一种情况:如图3,∵∠OQP=∠MOC+∠PAO+∠APQ,即∠OQP=m°+x°+n°①
∵∠OQP+∠CON+∠OBP+∠BPQ=360°,
∴∠OQP=360°﹣∠CON﹣∠OBP﹣∠BPQ,即∠OQP=360°﹣m°﹣y°﹣n°②,
①+②得2∠OQP=360°+x°﹣y°,
∴∠OQP=180°+![]() x°﹣
x°﹣![]() y°;
y°;

第二种情况:如图4,∵∠OQP+∠APQ=∠MOC+∠PAO,
即∠OQP+n°=m°+x°,
∴2∠OQP+2n°=2m°+2x°①,
∵∠APB=∠MON+∠PAO+∠PBO,
∴2n°=2m°+x°+y°②,
①﹣②得2∠OQP=x°﹣y°,
∴∠OQP=![]() x°﹣
x°﹣![]() y°,
y°,
综上所述,∠OQP=180°+![]() x°﹣
x°﹣![]() y°或∠OQP=
y°或∠OQP=![]() x°﹣
x°﹣![]() y°.
y°.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】攀枝花芒果由于品质高、口感好而闻名全国,通过优质快捷的网络销售渠道,小明的妈妈先购买了2箱A品种芒果和3箱B品种芒果,共花费450元;后又购买了l箱A品种芒果和2箱B品种芒果,共花费275元(每次两种芒果的售价都不变).
(1)问A品种芒果和B品种芒果的售价分别是每箱多少元?
(2)现要购买两种芒果共18箱,要求B品种芒果的数量不少于A品种芒果数量的2倍,但不超过A品种芒果数量的4倍,请你设计购买方案,并写出所需费用最低的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,请你判断∠1+∠2与∠A的关系?直接写出结论,不必说明理由.
思考(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=130°,求∠BIC的度数;
应用(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC.
(1)用直尺和圆规作∠A的平分线所在的直线![]() 和边BC的垂直平分线
和边BC的垂直平分线![]() (要求:不写作法,保留画图痕迹);
(要求:不写作法,保留画图痕迹);
(2)设(1)中的直线![]() 和直线
和直线![]() 交于点P,过点P作PE⊥AB,垂足为点E,过点P作PF⊥AC交AC的延长线于点F.请探究BE和CF的数量关系,并说明理由.
交于点P,过点P作PE⊥AB,垂足为点E,过点P作PF⊥AC交AC的延长线于点F.请探究BE和CF的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
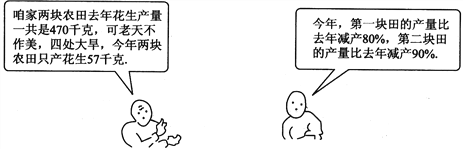
【题目】2010年春季我国西南大旱,导致大量农田减产,如图所示是一对农民父子的对话内容,请根据对话内容分别求出该农户今年两块农田的花生产量分别是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[﹣2.5]=﹣3;用<a>表示大于a的最小整数,例如:<2.5>=3,<4>=5,<﹣1.5>=﹣1.解决下列问题:
(1)[﹣4.5]=________,<3.5>=________.
(2)若[x]=2,则x的取值范围是________;若<y>=﹣1,则y的取值范围是________.
(3)已知x,y满足方程组 ,求x,y的取值范围.
,求x,y的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com