
 如图,将直线$y=\frac{{\sqrt{3}}}{3}x$向上平移2个单位交坐标轴于点A、D,然后绕AD中点B逆时针旋转60°,三条直线与y轴围成四边形ABCO,若四边形始终覆盖着二次函数y=x2-2mx+m2-1图象的一部分,则满足条件的实数m的取值范围为-$\sqrt{3}$-$\sqrt{2}$≤m≤$\sqrt{3}$.
如图,将直线$y=\frac{{\sqrt{3}}}{3}x$向上平移2个单位交坐标轴于点A、D,然后绕AD中点B逆时针旋转60°,三条直线与y轴围成四边形ABCO,若四边形始终覆盖着二次函数y=x2-2mx+m2-1图象的一部分,则满足条件的实数m的取值范围为-$\sqrt{3}$-$\sqrt{2}$≤m≤$\sqrt{3}$. 分析 将所给的抛物线解析式化为顶点式,可得:y=(x-m)2-1,由于m的值不确定,因此该函数的顶点在直线y=-1上左右移动;求四边形覆盖二次函数时m的取值范围,可考虑两种情况:①当抛物线对称轴右侧图象经过点B时,m的值;②当抛物线对称轴左侧图象经过点A时,m的值;联立上述两种情况下m的取值即可求得实数m的取值范围.
解答 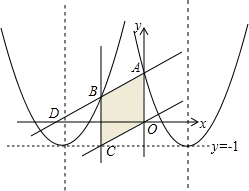 解:∵将直线$y=\frac{{\sqrt{3}}}{3}x$向上平移2个单位得到直线$y=\frac{{\sqrt{3}}}{3}x$+2,
解:∵将直线$y=\frac{{\sqrt{3}}}{3}x$向上平移2个单位得到直线$y=\frac{{\sqrt{3}}}{3}x$+2,
∴x=0时,y=2;y=0时,x=-2$\sqrt{3}$;
∴A(0,2),D(-2$\sqrt{3}$,0),
∵B是AD的中点,
∴B(-$\sqrt{3}$,1).
∵y=x2-2mx+m2-1=(x-m)2-1,
∴抛物线顶点在直线y=-1上移动;
假设四边形的边界可以覆盖到二次函数,则B点和A点分别是二次函数与四边形接触的边界点;
将B(-$\sqrt{3}$,1)代入二次函数,
解得m=-$\sqrt{3}$-$\sqrt{2}$,m=-$\sqrt{3}$+$\sqrt{2}$(不合题意,舍去);
将A(0,2)代入二次函数,
解得m=$\sqrt{3}$,b=-$\sqrt{3}$(不合题意,舍去);
所以实数m的取值范围是-$\sqrt{3}$-$\sqrt{2}$≤m≤$\sqrt{3}$.
故答案为-$\sqrt{3}$-$\sqrt{2}$≤m≤$\sqrt{3}$.
点评 此题考查了二次函数的性质,一次函数图象与几何变换,函数图象上点的坐标意义等知识,能够正确的判断出抛物线的移动范围是解决问题的关键.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
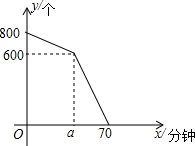 在妇女节前后,某快递总站的快递数量不断增加,每个快递到达总站后都需要进行快递单号的扫描,妇女节当天的早上,快递总站在进行快递单号扫描前,已收到800个未扫描快递,在扫描机开始工作后,仍平均每分钟有10个未扫描快递到达快递总站,扫描机平均每分钟扫描15个快递单号.已知在扫描机开始工作a分钟内只用一台扫描机工作.在妇女节当天未扫描的快递个数y(个)与扫描机工作时间x(分钟)之间的关系如图所示.
在妇女节前后,某快递总站的快递数量不断增加,每个快递到达总站后都需要进行快递单号的扫描,妇女节当天的早上,快递总站在进行快递单号扫描前,已收到800个未扫描快递,在扫描机开始工作后,仍平均每分钟有10个未扫描快递到达快递总站,扫描机平均每分钟扫描15个快递单号.已知在扫描机开始工作a分钟内只用一台扫描机工作.在妇女节当天未扫描的快递个数y(个)与扫描机工作时间x(分钟)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
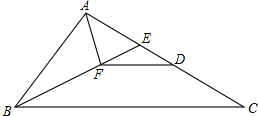 推理填空:完成下列证明:如图,E在△ABC的边AC上,且∠ABF=∠C,AF平分∠BAE交BE于点F,FD∥BC交AC于D.求证:AC-AB=DC.
推理填空:完成下列证明:如图,E在△ABC的边AC上,且∠ABF=∠C,AF平分∠BAE交BE于点F,FD∥BC交AC于D.求证:AC-AB=DC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com