
【题目】如图Ⅰ,已知:AD=AB,AD⊥AB,AC=AE,AC⊥AE.

(1)若反向延长△ABC的高AM交DE于点N,过D作DH⊥MN.求证:①DH=AM;②DN=EN
(2)如图Ⅱ,若AM为△ABC的中线,反向延长AM交DE于点N,求证:AN⊥DE.
【答案】(1)①见解析;②见解析;(2)见解析.
【解析】
(1)①利用AAS证明△ADH≌△BAM,可推出DH=AM;
②作EF⊥MN交MN的延长线于F,同法可证EF=AM,推出DH=EF,然后利用AAS证明△DNH≌△ENF即可;
(2)延长AM到F,使得MF=AM,证明四边形ABCF是平行四边形,再证明△ADE≌△CFA,得到∠E=∠CAF,由∠CAF+∠EAN=90°,推出∠EAN+∠E=90°,得到∠ANE=90°,即可求解.
(1)证明:①∵∠BAD=∠AHD=∠AMB=90°,
∴∠DAH+∠BAM=90°,∠DAH+∠ADH=90°,
∴∠BAM=∠ADH,
∵AB=AD,
∴△ADH≌△BAM(AAS),
∴DH=AM;
②如图,作EF⊥MN交MN的延长线于F,
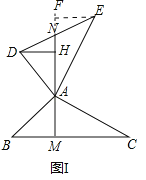
同①可证EF=AM,
∵DH=AM,
∴DH=EF,
∵∠DHN=∠EFN,∠DNH=∠ENF,
∴△DNH≌△ENF(AAS),
∴DN=EN;
(2)如图,延长AM到F,使得MF=AM,
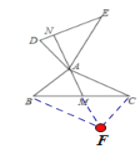
∵AM=MF,BM=CM,
∴四边形ABFC是平行四边形,
∴AB=CF,AB∥CF,
∴∠BAC+∠ACF=180°,
∵AD⊥AB, AC⊥AE
∴∠BAD=∠EAC=180°,
∴∠BAC+∠DAE=180°,
∴∠DAE=∠ACF,
∵AD=CF,AE=AC,
∴△ADE≌△CFA,
∴∠E=∠CAF,
∵∠CAF+∠EAN=90°,
∴∠EAN+∠E=90°,
∴∠ANE=90°,
∴AN⊥DE.


科目:初中数学 来源: 题型:
【题目】如图,大树AB与大数CD相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为90°,且EA=ED.已知大树AB的高为5m,小华行走的速度为1m/s,小华行走到点E的时间是( )

A. 13s B. 8s C. 6s D. 5s
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲于某日下午1时骑自行车从A地出发前往B地,乙于同日下午骑摩托车从A地出发前往B地,如图所示,图中折线PQR和线段MN分别表示甲和乙所行驶的路程和时间之间的关系图象,试根据图象回答下列问题.
(1)A、B两地相距多少千米?甲出发几小时,乙才开始出发?
(2)甲骑自行车的平均速度是多少?乙骑摩托车的平均速度是多少?
(3)乙在该日下午几时追上了甲?这时两人离B地还有多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[x]表示不超过x的最大整数,例如[﹣3.5]=﹣4,[2.1]=2,若y=x﹣[x],下列命题:①当x=﹣0.5时,y=0.5;②y的取值范围是:0≤y≤1;③对于所有的自变量x,函数值y随着x增大而一直增大.其中正确命题有 (只填写正确命题的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个三角形的两条边长为1cm和2cm,一个内角为45°.
(1)请你利用如图45°角,画出一个满足题设条件的三角形.
(2)你是否还能画出既满足题设条件,又与(1)中所画的不全等的三角形?若能,请用“尺规作图”画出,若不能,请说明理由.
(3)如果将题设条件改为“一个三角形的两条边长为3cm和4cm,一个内角为45°”,画出满足这一条件的,且彼此不全等的所有三角形.(要求在图中标记3cm和4cm的边长)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:两个二次项系数之和为1,对称轴相同,且图象与y轴交点也相同的二次函数互为友好同轴二次函数![]() 例如:
例如:![]() 的友好同轴二次函数为
的友好同轴二次函数为![]() .
.
![]() 请你分别写出
请你分别写出![]() ,
,![]() 的友好同轴二次函数;
的友好同轴二次函数;
![]() 满足什么条件的二次函数没有友好同轴二次函数?满足什么条件的二次函数的友好同轴二次函数是它本身?
满足什么条件的二次函数没有友好同轴二次函数?满足什么条件的二次函数的友好同轴二次函数是它本身?
![]() 如图,二次函数
如图,二次函数![]() :
:![]() 与其友好同轴二次函数
与其友好同轴二次函数![]() 都与y轴交于点A,点B、C分别在
都与y轴交于点A,点B、C分别在![]() 、
、![]() 上,点B,C的横坐标均为
上,点B,C的横坐标均为![]() ,它们关于
,它们关于![]() 的对称轴的对称点分别为
的对称轴的对称点分别为![]() ,
,![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,CB.
,CB.
![]() 若
若![]() ,且四边形
,且四边形![]() 为正方形,求m的值;
为正方形,求m的值;
![]() 若
若![]() ,且四边形
,且四边形![]() 的邻边之比为1:2,直接写出a的值.
的邻边之比为1:2,直接写出a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是-块长方形空地,长为![]() 米,宽为
米,宽为![]() 米,现要对其进行修整,在空白部分铺设
米,现要对其进行修整,在空白部分铺设![]() 条宽度为
条宽度为![]() 米的小路,其余阴影部分种植草坪.
米的小路,其余阴影部分种植草坪.

(1)用整式表示小路的面积;
(2)用整式表示草坪的面积;
(3)现有两种修整方案,方案一:修建小路的宽度为![]() 米;方案二:修建小路的宽度为
米;方案二:修建小路的宽度为![]() 米.铺设小路的造价为每平方米
米.铺设小路的造价为每平方米![]() 元,种植草坪的造价为每平方米
元,种植草坪的造价为每平方米![]() 元,请问选用哪种方案最划算.( 写出计算过程)
元,请问选用哪种方案最划算.( 写出计算过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点.
的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点.
(1)求m的值及C点坐标;
(2)在直线BC上方的抛物线上是否存在一点M,使得它与B,C两点构成的三角形面积最大,若存在,求出此时M点坐标;若不存在,请简要说明理由;
(3)P为抛物线上一点,它关于直线BC的对称点为Q.
①当四边形PBQC为菱形时,求点P的坐标;
②点P的横坐标为t(0<t<4),当t为何值时,四边形PBQC的面积最大,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在矩形MNPQ中,动点R从点N出发,沿着![]() 方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图②所示,那么下列说法不正确的是( )
方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图②所示,那么下列说法不正确的是( )

A.矩形MNPQ的周长是18B.当x=2时,y=5
C.当x=6时,y=10D.当y=8时,x=10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com