
分析 (1)首先把方程化为ax2+bx+c=0(a≠0)的形式,再根据a叫做二次项系数;b叫一次项系数;c叫做常数项进行解答;
(2)首先把方程化为ax2+bx+c=0(a≠0)的形式,再根据a叫做二次项系数;b叫一次项系数;c叫做常数项进行解答;
(3)首先把方程化为ax2+bx+c=0(a≠0)的形式,再根据a叫做二次项系数;b叫一次项系数;c叫做常数项进行解答;
(4)首先把方程化为ax2+bx+c=0(a≠0)的形式,再根据a叫做二次项系数;b叫一次项系数;c叫做常数项进行解答.
解答 解:(1)5x2-1=4x,
5x2-4x-1=0,
二次项系数为5,一次项系数为-4,常数项为-1;
(2)4x2=81,
4x2-81=0,
二次项系数为4,一次项系数为0,常数项为-81;
(3)4x(x+2)=25,
4x2+8x-25=0,
二次项系数为4,一次项系数为8,常数项为-25;
(4)(3x-2)(x+1)=8x-3.
整理得:3x2-7x+1=0,
二次项系数为3,一次项系数为-7,常数项为1.
点评 此题主要考查了一元二次方程的一般形式,关键是掌握任何一个关于x的一元二次方程经过整理,都能化成如下形式ax2+bx+c=0(a≠0).这种形式叫一元二次方程的一般形式.其中ax2叫做二次项,a叫做二次项系数;bx叫做一次项;c叫做常数项.


科目:初中数学 来源: 题型:解答题
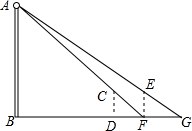 如图,河对岸有一路灯杆AB,在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己的影长FG=4m.如果小明的身高为1.7m,求路灯杆AB的高度.
如图,河对岸有一路灯杆AB,在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己的影长FG=4m.如果小明的身高为1.7m,求路灯杆AB的高度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com