
【题目】如图,直线AB、CD、EF相交于点O . 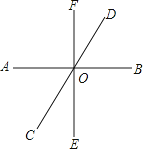
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
【答案】
(1)
【解答】∠COE的邻补角为∠COF和∠EOD
(2)
【解答】∠COE和∠BOE的对顶角分别为∠DOF和∠AOF
(3)
【解答】∵∠BOF=90°,
∴AB⊥EF
∴∠AOF=90°,
又∵∠AOC=∠BOD=60°
∴∠FOC=∠AOF+∠AOC=90°+60°=150°.
【解析】(1)根据邻补角的概念即可解答;(2)根据对顶角的概念即可解答;(3)因为∠BOF=90°,所以AB⊥EF , 由此可得∠AOF , 再根据对顶角的概念可得∠FOC的度数.
【考点精析】解答此题的关键在于理解对顶角和邻补角的相关知识,掌握两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个.


科目:初中数学 来源: 题型:
【题目】已知A=x-y+1,B=x+y+1,C=(x+y)(x-y)+2x,两同学对x、y分别取了不同的值,求出的A、B、C的值不同,但A×B-C的值却总是一样的.因此两同学得出结论:无论x、y取何值,A×B-C的值都不发生变化.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,AB=10厘米,BC=8厘米,CD=12厘米,∠B=∠C,点E为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动. 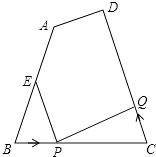
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPE与△CQP是否全等?请说明理由.
(2)当点Q的运动速度为多少时,能够使△BPE与△CQP全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民用电的电价实行阶梯收费,收费标准如下表:

(1)已知李叔家四月份用电286度,缴纳电费178.76元;五月份用电316度,缴纳电费198.56元,请你根据以上数据,求出表格中a,b的值.
(2)六月份是用电高峰期,李叔计划六月份电费支出不超过300元,那么李叔家六月份最多可用电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,下列结论中不正确的是--------------------( )
A. 当AB=BC时,它是菱形 B. 当AC=BD时,它是正方形
C. 当∠ABC=90°时,它是矩形 D. 当AC⊥BD时,它是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F分别是AD和BC上的两点,EF将四边形ABCD分成两个边长为5cm的正方形,∠DEF=∠EFB=∠B=∠D=90°;点H是CD上一点且CH=lcm,点P从点H出发,沿HD以lcm/s的速度运动,同时点Q从点A出发,沿A→B→C以5cm/s的速度运动.任意一点先到达终点即停止运动;连结EP、EQ.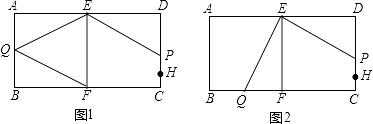
(1)用t表示△EPD的面积;
(2)试探究:当t为何值时,△EPD的面积等于△EQF面积的 ![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由大小两种货车,3辆大车与4辆小车一次可以运货22吨,2辆大车与6辆小车一次可以运货23吨.请根据以上信息,提出一个能用方程(组)解决的问题,并写出这个问题的解答过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com