证明:
(1)∵DC=BC,∠1=∠2,CF=CF,
∴△DFC≌△BFC(SAS).
(2)延长DF交BC于G,

∵AD∥BG,AB∥DG,
∴四边形ABGD为平行四边形.
∴AD=BG.
∵△DFC≌△BFC,
∴∠EDF=∠GBF,DF=BF.
又∵∠3=∠4,
∴△DFE≌△BFG.
∴DE=BG,EF=GF.
∴AD=DE.
(3)∵EF=GF,DF=BF,
∴EF+BF=GF+DF,即:BE=DG.
∵DG=AB,
∴BE=AB.
∵C
△DFE=DF+FE+DE=6,
∴BF+FE+DE=6,即:EB+DE=6.
∴AB+AD=6.
又∵AD=2,
∴AB=4.
∴DG=AB=4.
∵BG=AD=2,
∴GC=BC-BG=5-2=3.
又∵DC=BC=5,
在△DGC中∵4
2+3
2=5
2∴DG
2+GC
2=DC
2∴∠DGC=90°.
∴S
梯形ABCD=

(AD+BC)•DG
=

(2+5)×4
=14.
分析:(1)根据CF平分∠BCD,可知:∠1=∠2,又DC=BC,CF=CF,可证:△DCF≌△BCF;
(2)作辅助线,延长DF交BC于G,由AD∥BG,AB∥DG,可知:四边形ABGD为平行四边形,AD=BG,故证AD=DE只需证明BG=DE,由(1)可知:∠EDF=∠GBF,DF=BF,对顶角∠3=∠4,可证:△DFE≌△BFG,BG=DE,从而可证:AD=DE;
(3)由(1)(2)可知:EF=GF,DF=BF,可得:BE=DG,根据C
△DFE=6,可得:EB+DE=AB+AD=6,已知AD的长,可求出AB,又AD=BG,BC=DC=5,可得CG=3,根据勾股定理逆定理可得:△DGC为直角三角形,即DG为梯形的高,代入梯形面积公式:S=

(AD+BC)•DG计算即可.
点评:本题主要考查梯形性质的应用,求梯形的面积时关键是证明△DGC为直角三角形.


 (AD+BC)•DG
(AD+BC)•DG (2+5)×4
(2+5)×4 (AD+BC)•DG计算即可.
(AD+BC)•DG计算即可.

 阅读快车系列答案
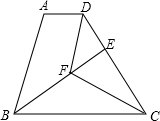
阅读快车系列答案 (2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G.
(2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G. 已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.
已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.