
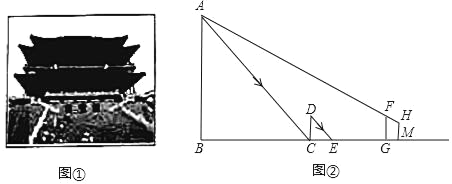
【题目】大唐芙蓉园是中国第一个全方位展示盛唐风貌的大型皇家园林式文化主题公园,全园标志性建筑一紫云楼为代表,展示了“形神升腾紫云景,天下臣服帝王心”的唐代帝王风范(如图①).小风和小花等同学想用一些测量工具和所学的几何知识测量“紫云楼”的高度,来检验自己掌握知识和运用知识的能力,他们经过研究需要两次测量:首先,在阳光下,小风在紫云楼影子的末端C点处竖立一根标杆CD,此时,小花测得标杆CD的影长CE=2米,CD=2米;然后,小风从C点沿BC方向走了5.4米,到达G处,在G处竖立标杆FG,接着沿BG后退到点M处时,恰好看见紫云楼顶端A,标杆顶端F在一条直线上,此时,小花测得CM=0.6米,小风的眼睛到地面的距离HM=1.5米,FG=2米.
如图②,已知AB⊥BM,CD⊥BM,FG⊥BM,HM⊥BM,请你根据题中提供的相关信息,求出紫云楼的高AB.
科目:初中数学 来源: 题型:
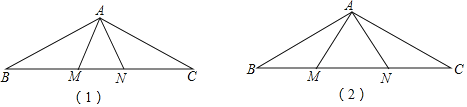
【题目】已知如图,M、N是△ABC的BC边上两点,且AB=AC,BM=CN
(1)如图1,证明:△ABN≌△ACM;
(2)如图2,当∠ANB=2∠B时,直接写出图中所有等腰三角形(△ABC除外)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:平面内,如果一个四边形的四个顶点到某一点的距离都相等,则称这一点为该四边形的外心.
(1)下列四边形:平行四边形、矩形、菱形中,一定有外心的是 ;
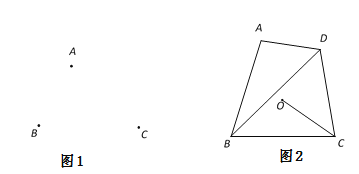
(2)已知四边形ABCD有外心O,且A,B,C三点的位置如图1所示,请用尺规确定该四边形的外心,并画出一个满足条件的四边形ABCD;
(3)如图2,已知四边形ABCD有外心O,且BC=8,sin∠BDC=![]() ,求OC的长.
,求OC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
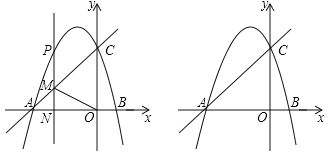
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,与y轴交于C.直线y=
x2+bx+c与x轴交于A、B两点,与y轴交于C.直线y=![]() x+3经过点A、C.
x+3经过点A、C.
(1)求抛物线的解析式;
(2)P是抛物线上一动点,过P作PM∥y轴交直线AC于点M,设点P的横坐标为t.
①若以点C、O、M、P为顶点的四边形是平行四边形,求t的值.
②当射线MP,AC,MO中一条射线平分另外两条射线的夹角时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=60°,在∠AOB的平分线OM上有一点C,将一个120°角的顶点与点C重合,它的两条边分别与直线OA、OB相交于点D、E.
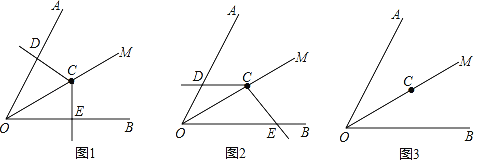
(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OE+OD与OC的数量关系,并说明理由;
(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;
(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,上述结论是否成立?请在图3中画出图形,若成立,请给于证明;若不成立,线段OD、OE与OC之间又有怎样的数量关系?请写出你的猜想,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
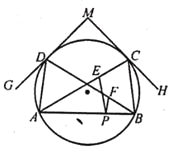
【题目】如图,⊙O的半径为4,A,B,C,D是⊙O上的四点,过点C,D的切线CH,DG相交于点M,点P在弦AB上,PE∥BC交AC于点E,PF∥AD于点F,当∠ADG=∠BCH=30°时,PE+PF的值是( )
A. 4B. 2 ![]() C. 4
C. 4 ![]() D. 不确定
D. 不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.
(1) 试判断BE与FH的数量关系,并说明理由;
(2) 求证:∠ACF=90°;
(3) 连接AF,过A,E,F三点作圆,如图2. 若EC=4,∠CEF=15°,求![]() 的长.
的长.

图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
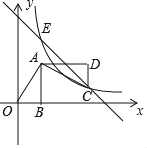
【题目】如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=![]() 的一个分支上,过C点的直线y=﹣x+b与双曲线的另一个交点为E,则△EOC的面积为_____.
的一个分支上,过C点的直线y=﹣x+b与双曲线的另一个交点为E,则△EOC的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
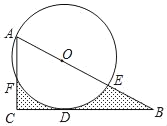
【题目】如图,点O是Rt△ABC斜边AB上的一点,⊙O经过点A与BC相切于点D,分别交AB,AC于E,F,OA=2cm,AC=3cm.
(1)求BE的长;
(2)求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com