已知关于x的方程x2-(2k-3)x+k2+1=0.
(1)当k满足什么条件时,此方程有实数根?
(2)若此方程的两个实数根x1、x2满足:2|x1|=5-2|x2|,求k的值.
解:(1)依题意△=[-(2k-3)]
2-4×(k
2+1)≥0
解得:k≤
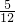
;
(2)由根与系数的关系可知x
1+x
2=2k-3,x
1x
2=k
2+1,
∴x
1、x
2同号,
①当x
1>0,x
2>0时,由2|x
1|=5-2|x
2|得,
2(x
1+x
2)=5 即 2(2k-3)=5,
∴k=
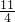
∵k≤
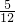
∴

不合题意,(舍去),
②当x
1<0,x
2<0时,由2|x
1|=5-2|x
2|得
2(x
1+x
2)=-5 即 2(2k-3)=-5
∴k=

综合①、②可知 k=

.
分析:(1)利用一元二次方程的根的判别式就可以得到关于k的不等式,解不等式即可求出k的取值范围;
(2)先利用根与系数的关系判断出x
1、x
2同号,再根据2|x
1|=5-2|x
2|,可以得到关于k的方程,然后解方程即可求出k的值.
点评:此题考查了一元二次方程根的判别式,解答此题要知道一元二次方程根的情况与判别式△的关系(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根;一元二次方程根与系数的关系:(1)x
1+x
2=-

,(2)x
1x
2=

.

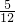 ;
;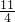
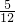
 不合题意,(舍去),
不合题意,(舍去),
 .
. ,(2)x1x2=
,(2)x1x2= .
. 
