练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

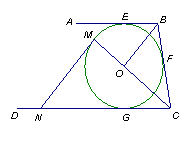
    如图，AB、BC、CD分别与⊙O切于E、F、G，且AB∥CD。连接OB、OC，延长CO交⊙O于点M，过点M作MN∥OB交CD于N。（1）求证：MN是⊙O的切线；

    （2）当0B=6cm，OC=8cm时，求⊙O的半径及MN的长。


    解：（1）证明：∵AB、BC、CD分别与⊙O切于点E、F、G，

    ∴  

    ∵AB∥CD，∴∠ABC＋∠DCB＝180°．

    ∴

    ∴   

    ∵MN∥OB，∴∠NMC＝∠BOC＝90°．∴MN是⊙O的切线．

    （2）连接OF，则OF⊥BC．

    由⑴知，△BOC是Rt△，∴   

       ∵

    ∴6×8＝10×OF．∴0F＝4.8．即⊙O的半径为4.8cm  

    由⑴知，∠NCM＝∠BCO，∠NMC＝∠BOC＝90°，

    ∴△NMC∽△BOC.　

    ∴

    ∴MN＝9.6(cm)  


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    一个30°的直角三角板的斜边长为5cm，把这个三角板绕斜边旋转360°，求所得的几何体的表面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，直三棱柱的底面为正三角形，且主视图是边长为4的正方形，则此直三棱柱左视图的面积为          。（改编）

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图是有关X的代数式的方阵，若第10行第2项的值为1034，则此时X的值为（　  ）

    A.10        B.1         C.5        D.2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在Rt△ABC中，AB＝6，AC＝8， P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，

    求△AEF面积最大为            。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一只盒子中有红球m个，白球8个，黑球n个，每个球除颜色外都相同，从中任取一个球，取得是白球的概率与不是白球的概率相同，那么m与n的关系是     (    )

    (A) m + n = 8    (B) m + n = 4   (C) m = n = 4    (D) m = 3，n =5

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     下面有4个正整数的集合： (1)1～97中3的倍数； (2)1～97中4的倍数；(3)1～97中5的倍数；(4)l～97中6的倍数．其中平均数最大的集合是（       ）

    (A) (1)            (B) (2)             (C) (3)                (D ) (4)

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知如图直线∥，且 则           (      )  

    A.110°　　 B.120°   　C.130°      D.140°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABC中，∠BAC=90°，正方形的一边GF在BC上，其余两个顶点D，E分别在AB，AC上.连接AG，AF分别交DE于M，N两点．

    （1）求证：.（改编2012上城区二模试卷22题）

    (2) 求证：．

    (3)若AB=AC=4，求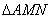与的面积之比

     

    查看答案和解析>>

    同步练习册答案