
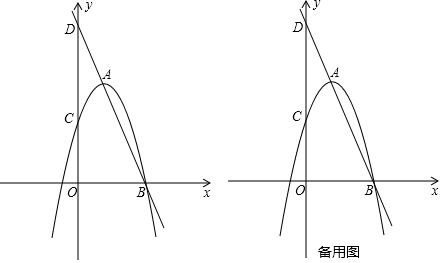
分析 (1)把A点坐标代入直线解析式可求得m,则可求得B点坐标,再利用待定系数法可求得抛物线解析式;
(2)由全等三角形的性质可得到OP是第三象限的角平分线,可设出P点坐标,求得其坐标;
(3)可设Q(0,y),由勾股定理可分别表示出AQ、BQ和AB长,分∠AQB=90°、∠ABQ=90°和∠BAQ=90°三种情况,分别利用勾股定理得到关于y的方程,可求得y的值,则可求得Q点的坐标.
解答 解:
(1)∵直线y=-3x+m经过A点,
∴9=-6+m,解得m=15,
∴直线表达式为y=-3x+15,
令y=0可得-3x+15=0,解得x=5,
∴B(5,0),
∵抛物线y=ax2+bx+c的顶点A的坐标为(2,9),
∴可设抛物线解析式为y=a(x-2)2+9,
∵抛物线过点B,
∴0=a(5-2)2+9,解得a=-1,
∴抛物线解析式为y=-(x-2)2+9,即y=-x2+4x+5;
(2)在y=-x2+4x+5中,令x=0可得y=5,
∴C(0,5),
∴OB=OC=5,
∵OP=OP,
∴当△POB≌△POC时可知∠POB=∠POC,
∴OP是第三象限的角平分线,
∵点P为抛物线在第三象限图象上的一点,
∴可设点P的坐标为(x,-x2+4x+5)(x<0),
则有x=-x2+4x+5,解得x=$\frac{3+\sqrt{29}}{2}$(不符合题意,舍去)或x=$\frac{3-\sqrt{29}}{2}$,
∴P点坐标为($\frac{3-\sqrt{29}}{2}$,$\frac{3-\sqrt{29}}{2}$);
(3)设Q点坐标为(0,y),
∵A(2,9),B(5,0),
∴AQ2=(0-2)2+(y-9)2=y2-18y+85,BQ2=(0-5)2+y2=y2+25,AB2=(2-5)2+92=90,
∵△ABQ为直角三角形,
∴有∠AQB=90°、∠ABQ=90°和∠BAQ=90°三种情况,
①当∠AQB=90°时,则有AQ2+BQ2=AB2,即y2-18y+85+y2+25=90,解得y=$\frac{9+\sqrt{41}}{2}$或y=$\frac{9-\sqrt{41}}{2}$,此时Q点坐标为(0,$\frac{9+\sqrt{41}}{2}$)或(0,$\frac{9-\sqrt{41}}{2}$);
②当∠ABQ=90°时,则有AB2+BQ2=AQ2,即90+y2+25=y2-18y+85,解得y=-$\frac{5}{3}$,此时Q点的坐标为(0,-$\frac{5}{3}$);
③当∠BAQ=90°时,则有AB2+AQ2=BQ2,即90+y2-18y+85=y2+25,解得y=$\frac{25}{3}$,此时Q点的坐标为(0,$\frac{25}{3}$);
综上可知Q点的坐标为(0,$\frac{9+\sqrt{41}}{2}$)或(0,$\frac{9-\sqrt{41}}{2}$)或(0,-$\frac{5}{3}$)或(0,$\frac{25}{3}$).
点评 本题为二次函数的综合应用,涉及待定系数法、全等三角形的性质、勾股定理、方程思想及分类讨论思想等知识.在(1)中求得B点坐标是解题的关键,注意待定系数法的应用,在(2)中根据全等三角形的性质确定出OP是第三象限的角平分线是解题的关键,在(3)中用Q的坐标表示AQ、BQ的长是解题的关键.本题考查知识点较多,综合性较强,难度适中.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,从一个直径是2m的圆形铁皮中剪出一个圆心角为90°的扇形,如果将剪下来的扇形围成一个圆锥,那么圆锥的高等于$\frac{\sqrt{30}}{4}$m.
如图,从一个直径是2m的圆形铁皮中剪出一个圆心角为90°的扇形,如果将剪下来的扇形围成一个圆锥,那么圆锥的高等于$\frac{\sqrt{30}}{4}$m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
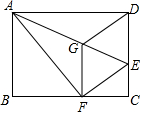 如图,将矩形ABCD沿AE折叠,点D的对应点落在BC上点F处,过点F作FG∥CD,连接EF,DG,下列结论中正确的有( )
如图,将矩形ABCD沿AE折叠,点D的对应点落在BC上点F处,过点F作FG∥CD,连接EF,DG,下列结论中正确的有( )| A. | ①②③④ | B. | ①②③ | C. | ①③④ | D. | ①② |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{频数}{组距}$ | B. | $\frac{频率}{组距}$ | C. | $\frac{频率}{组数}$ | D. | $\frac{频数}{组数}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
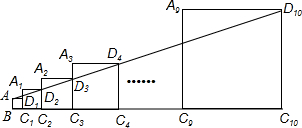 已知正方形ABC1D1的边长为1,延长C1D1到A1,以A1C1为边向右作正方形A1C1C2D2,延长C2D2到A2,以A2C2为边向右作正方形A2C2C3D3(如图所示),以此类推….若A1C1=2,且点A,D2,D3,…,Dn+1都在同一直线上,则正方形AnCnCn+1Dn+1的边长是$\frac{{3}^{n-1}}{{2}^{n-2}}$.
已知正方形ABC1D1的边长为1,延长C1D1到A1,以A1C1为边向右作正方形A1C1C2D2,延长C2D2到A2,以A2C2为边向右作正方形A2C2C3D3(如图所示),以此类推….若A1C1=2,且点A,D2,D3,…,Dn+1都在同一直线上,则正方形AnCnCn+1Dn+1的边长是$\frac{{3}^{n-1}}{{2}^{n-2}}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com