
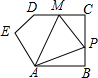
 在五边形ABCDE中,∠B=90°,AB=BC=CD=1,AB∥CD,M是CD边的中点,点P由点A出发,按A→B→C→M的顺序运动.设点P经过的路程x为自变量,△APM的面积为y,则函数y的大致图象是( )
在五边形ABCDE中,∠B=90°,AB=BC=CD=1,AB∥CD,M是CD边的中点,点P由点A出发,按A→B→C→M的顺序运动.设点P经过的路程x为自变量,△APM的面积为y,则函数y的大致图象是( )| A. | 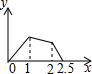 | B. | 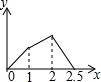 | C. | 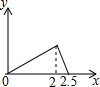 | D. | 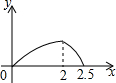 |
分析 根据已知条件,可以分别求出各段对应的函数解析式,从而可以得到各段对应的函数图象,从而可以解答本题.
解答 解:由已知可得,
当点P从A到B的过程中,y=$\frac{x×1}{2}=\frac{x}{2}$(0≤x≤1);
当点P从B到C的过程中,y=$\frac{(\frac{1}{2}+1)×1}{2}-\frac{1×(x-1)}{2}-\frac{\frac{1}{2}×(2-x)}{2}$=$\frac{3}{4}-\frac{x-1}{2}-\frac{2-x}{4}$=$\frac{-x+3}{4}$(1≤x≤2);
点P从C到M的过程中,y=$\frac{(2+\frac{1}{2}-x)×1}{2}=-\frac{x}{2}+\frac{5}{4}$(2≤x≤$\frac{5}{2}$).
故选A.
点评 本题考查动点问题的函数图象,解题的关键是明确题意,可以求出各段的函数解析式.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点B逆时针旋转60°得到△A′BC′,连接A′C,则A′C的长为4+3$\sqrt{3}$.
如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点B逆时针旋转60°得到△A′BC′,连接A′C,则A′C的长为4+3$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2016x2015 | B. | 2016x2016 | C. | 4032x2015 | D. | 4032x2016 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC和△DCB中,AB=DC,AC=DB,AC与DB交于点M.
如图,在△ABC和△DCB中,AB=DC,AC=DB,AC与DB交于点M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com