
【题目】如图,在△ABC中,AC=AB,∠BAC=90°,D是AC边上一点,连接BD,AF⊥BD于点F,点E在BF上,连接AE,∠EAF=45°,连接CE,AK⊥CE于点K,交DE于点H,∠DEC=30°,HF=![]() ,则EC=______
,则EC=______
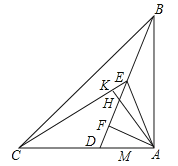
【答案】6
【解析】
延长AF交CE于P,证得△ABH≌△APC得出AH=CP,证得△AHF≌△EPF得出AH=EP,得出EC=2AH,解30°的直角三角形AFH求得AH,即可求得EC的长.
如图,延长AF交CE于P,
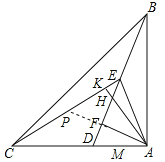
∵∠ABH+∠ADB=90°,∠PAC+∠ADB=90°,
∴∠ABH=∠PAC,
∵AK⊥CE,AF⊥BD,∠EHK=∠AHF,
∴∠HEK=∠FAH,
∵∠FAH+∠AHF=90°,∠HEK+∠EPF=90°,
∴∠AHF=∠EPF,
∴∠AHB=∠APC,
在△ABH与△APC中,
 ,
,
∴△ABH≌△APC(ASA),
∴AH=CP,
在△AHF与△EPF中,
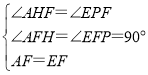 ,
,
∴△AHF≌△EPF(AAS),
∴AH=EP,∠CED=∠HAF,
∴EC=2AH,
∵∠DEC=30°,
∴∠HAF=30°,
∴AH=2FH=2×![]() =3,
=3,
∴EC=2AH=6.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】某校有1500名学生,小明想了解全校学生每月课外阅读书籍的数量情况,随机抽取了部分学生,得到如统计图:
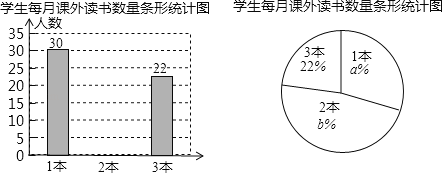
(1)一共抽查了多少人?
(2)每月课外阅读书籍数量是1本的学生对应的圆心角度数是多少?
(3)估计该校全体学生每月课外阅读书籍的总量大约是多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
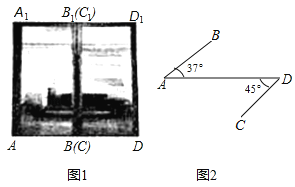
【题目】图1是一商场的推拉门,已知门的宽度![]() 米,且两扇门的大小相同(即
米,且两扇门的大小相同(即![]() ),将左边的门
),将左边的门![]() 绕门轴
绕门轴![]() 向里面旋转
向里面旋转![]() ,将右边的门
,将右边的门![]() 绕门轴
绕门轴![]() 向外面旋转
向外面旋转![]() ,其示意图如图2,求此时
,其示意图如图2,求此时![]() 与
与![]() 之间的距离(结果保留一位小数).(参考数据:
之间的距离(结果保留一位小数).(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a是最大的负整数,b、c满足![]() ,且a,b,c分别是点A,B,C在数轴上对应的数.
,且a,b,c分别是点A,B,C在数轴上对应的数.
(1)求a,b,c的值,并在数轴上标出点A,B,C;
![]()
(2)若动点P从C出发沿数轴正方向运动,点P的速度是每秒2个单位长度,运动几秒后,点P到达B点?
(3)在数轴上找一点M,使点M到A,B,C三点的距离之和等于13,请直接写出所有点M对应的数.(不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得的宽度,他们是这样做的:①在河流的一条岸边B点,选对岸正对的一棵树A;②沿河岸直走20m有一棵树C,继续前行20m到达D处;③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;④测得DE的长为5米.
(1)河的宽度是 米.
(2)请你说明他们做法的正确性.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,BA=BC,BD是△ABC的中线,△ABC的角平分线AE交BD于点F,过点C作AB的平行线交AE的延长线于点G
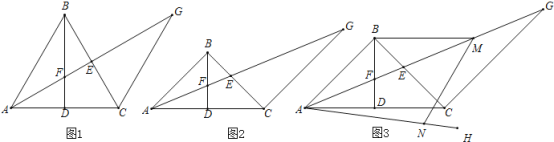
(1)如图1,若∠ABC=60°,求证:AF=![]() EG;
EG;
(2)如图2,若∠ABC=90°,求证:AF=![]() EG;
EG;
(3)在(2)的条件下如图3,过点A作∠CAH=![]() ∠FAC,过点B作BM∥AC交AG于点M,点N在AH上,连接MN、BN,若∠BMN+∠EAH=90°,
∠FAC,过点B作BM∥AC交AG于点M,点N在AH上,连接MN、BN,若∠BMN+∠EAH=90°,![]() ,求BN的长.
,求BN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点M为直线AB上一动点, ![]() 都是等边三角形,连接BN
都是等边三角形,连接BN
![]() 求证:
求证: ![]() ;
;
![]() 分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系
分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系![]() 不需证明
不需证明![]() ;
;
![]() 如图4,当
如图4,当![]() 时,证明:
时,证明: ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
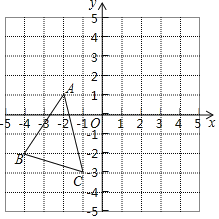
【题目】如图,△ABC中,A(-2,1),B(-4,-2),C(-1,-3),△A′B′C′是△ABC平移之后得到的图象,并且C的对应点C′的坐标为(4,1)
(1)A′、B′两点的坐标分别为A′______,B′______;
(2)作出△ABC平移之后的图形△A′B′C′;
(3)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com