
【题目】如图①所示是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
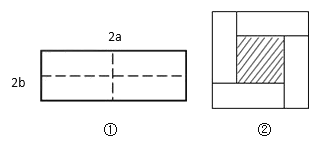
(1)图②中的阴影部分的正方形的边长等于 .(用含![]() ,
,![]() 的代数式表示)
的代数式表示)
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积:
方法①: .
方法②: .
(3)观察图②,直接写出![]() 、
、![]() 、
、![]() 这三个代数式之间的等量关系.
这三个代数式之间的等量关系.
(4)根据(3)题中的等量关系,若![]() ,
,![]() ,求图②中阴影部分的面积.
,求图②中阴影部分的面积.
【答案】(1)a-b;(2) (ab)2, (a+b)24ab;(3)(ab)2=(a+b)24ab;(4)8
【解析】
(1)根据阴影部分可得边长(a-b);
(2) 方法①:直接读取阴影部分正方形的边长是a-b,再求面积;
方法②:用(a+b)为边长的正方形面积减去四个矩形面积即可;
(3)由上题的两个方法的出等量关系式即可;
(4)将a+b=12,ab=20的值代入上题中的等量关系式,再求阴影部分的面积即可.
解: (1)根据图形可得:阴影部分的正方形的边长a-b,
故答案为a-b;
(2)根据图形可得:
方法①:(ab)2
方法②:(a+b)24ab
故答案为:(ab)2,(a+b)24ab.
(3)由阴影部分的两个面积代数式相等,
∴(ab)2=(a+b)24ab;
(4)由题意得:(ab)2=(a+b)24ab
将![]() ,
,![]() 代入上式得:(ab)2=1444×20=64,
代入上式得:(ab)2=1444×20=64,
∵a-b>0,
∴a-b=8,
∴图②中阴影部分的面积为8.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBEF是菱形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,![]() 的顶点都在网格点上,其中,
的顶点都在网格点上,其中,![]() 点坐标为
点坐标为![]() ,
,
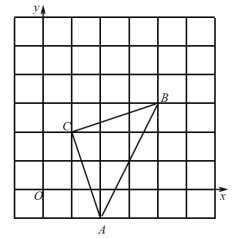
(1)写出点![]() 、
、![]() 的坐标:
的坐标:![]() (____,____)、
(____,____)、![]() (____,____)
(____,____)
(2)将![]() 先向左平移
先向左平移![]() 个单位长度,再向上平移
个单位长度,再向上平移![]() 个单位长度,得到
个单位长度,得到![]() ,画出
,画出![]() ;
;
(3)写出三个顶点坐标![]() (___,___)、
(___,___)、![]() (___,___)、
(___,___)、![]() (___,___);
(___,___);
(4)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
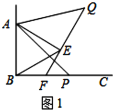
【题目】如图1,已知![]() ,
,![]() 是等边三角形,点
是等边三角形,点![]() 为射线
为射线![]() 上任意一点(点
上任意一点(点![]() 与点
与点![]() 不重合),连结
不重合),连结![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连结
,连结![]() 并延长交射线
并延长交射线![]() 于点
于点![]() .
.
(1)如图1,当![]() 时,
时,![]() ________
________![]() ,猜想
,猜想![]() ________
________![]() ;
;
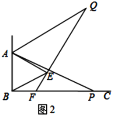
(2)如图2,当点![]() 为射线
为射线![]() 上任意一点时,猜想
上任意一点时,猜想![]() 的度数,并说明理由;
的度数,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆拥有客房90间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
x(元) | 200 | 240 | 270 | 300 |
y(间) | 90 | 70 | 55 | 40 |
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房,宾馆每日需支出60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入﹣当日支出)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA延长线上,∠FDA=∠B,AC=6,AB=8,则四边形AEDF的周长为( )

A. 16 B. 20 C. 18 D. 22
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读第(1)题解答过程填理由,并解答第(2)题
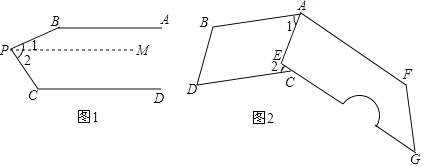
(1)已知:如图1,AB∥CD,P为AB,CD之间一点,求∠B+∠C+∠BPC的大小.
解:过点P作PM∥AB
∵AB∥CD(已知)
∴PM∥CD ,
∴∠B+∠1=180°, .
∴∠C+∠2=180°
∵∠BPC=∠1+∠2
∴∠B+∠C+∠BPC=360°
(2)我们生活中经常接触小刀,如图2小刀刀柄外形是一个直角梯形挖去一个小半圈,其中AF∥EG,∠AEG=90°,刀片上、下是平行的(AB∥CD),转动刀片时会形成∠1和∠2,那么∠1+∠2的大小是否会随刀片的转动面改变,如不改变,求出其大小;如改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=ax+b和反比例函数y= ![]() 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
A.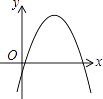
B.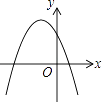
C.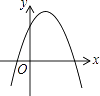
D.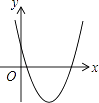
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com