
【题目】如图,Rt△ABO的顶点A是双曲线![]() 与直线
与直线![]() 在第二象限的交点,AB⊥轴于B且S△ABO =
在第二象限的交点,AB⊥轴于B且S△ABO =![]() .
.

(1)求这两个函数的解析式.
(2)求直线与双曲线的两个交点A,C和直线AC与x轴的交点D的坐标和△AOC的面积.
【答案】(1)![]() ,
,![]() ;(2)A(-1,3),C(3,-1),D(2,0),△AOC的面积=4.
;(2)A(-1,3),C(3,-1),D(2,0),△AOC的面积=4.
【解析】
(1)根据反比例函数解析式的比例系数k的几何意义,即可得到答案;
(2)联立 ,即可求出点A,C的坐标,在直线
,即可求出点A,C的坐标,在直线![]() 中,令y=0,即可得到D的坐标, 再分别求出
中,令y=0,即可得到D的坐标, 再分别求出![]() ,
,![]() 的面积,即可得到△AOC的面积.
的面积,即可得到△AOC的面积.
(1)∵Rt△ABO的顶点A是双曲线![]() 与直线
与直线![]() 在第二象限的交点,AB⊥轴于B且S△ABO =
在第二象限的交点,AB⊥轴于B且S△ABO =![]() ,
,
∴![]() ,
,
∵双曲线![]() 在二,四象限,
在二,四象限,
∴k<0,
∴k=-3,
∴反比例函数解析式为:![]() ,一次函数解析式为:
,一次函数解析式为:![]() ;
;
(2)联立 ,得:
,得:![]() ,
,
解得:![]() ,
,
当x=-1时,y=1+2=3;当x=3时,y=-3+2=-1,
∴A(-1,3),C(3,-1),
∴AB=3,
在直线![]() 中,令y=0,则
中,令y=0,则![]() ,解得:x=2,
,解得:x=2,
∴D(2,0),
∴OD=2,
过点C作CE⊥x轴于点E,则CE=1,
∴![]() ,
,![]() ,
,
∴△AOC的面积=![]() +
+![]() =1+3=4.
=1+3=4.



科目:初中数学 来源: 题型:
【题目】(1)①如图1,请用直尺(不带刻度)和圆规作出![]() 的内接正三角形
的内接正三角形![]() (按要求作图,不要求写作法,但要保留作图痕迹).
(按要求作图,不要求写作法,但要保留作图痕迹).
②若![]() 的内接正三角形
的内接正三角形![]() 边长为6,求
边长为6,求![]() 的半径;
的半径;
(2)如图2,![]() 的半径就是(1)中所求半径的值.点
的半径就是(1)中所求半径的值.点![]() 在
在![]() 上,
上,![]() 是
是![]() 的切线,点
的切线,点![]() 在射线
在射线![]() 上,且
上,且![]() ,点
,点![]() 从点
从点![]() 出发,以每秒1个单位的速度沿射线
出发,以每秒1个单位的速度沿射线![]() 方向移动,点
方向移动,点![]() 是
是![]() 上的点(不与点
上的点(不与点![]() 重合),
重合),![]() 是
是![]() 的切线.设点
的切线.设点![]() 运动的时间为
运动的时间为![]() (秒),当
(秒),当![]() 为何值时,
为何值时,![]() 是直角三角形,请你求出满足条件的所有
是直角三角形,请你求出满足条件的所有![]() 值.
值.

查看答案和解析>>
科目:初中数学 来源: 题型:
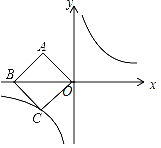
【题目】如图,在平面直角坐标系中,正方形ABCO的对角线BO在x轴上,若正方形ABCO的边长为4![]() ,点B在x负半轴上,反比例函数的图象经过C点.
,点B在x负半轴上,反比例函数的图象经过C点.
(1)求该反比例函数的解析式;
(2)若点P是反比例函数上的一点,且△PBO的面积恰好等于正方形ABCO的面积,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里有标号为![]() 的五个小球,除数字不同外,小球没有任何区别,摸球前先搅拌均匀,每次摸一个球.
的五个小球,除数字不同外,小球没有任何区别,摸球前先搅拌均匀,每次摸一个球.
(1)下列说法:
①摸一次,摸出一号球和摸出![]() 号球的概率相同;
号球的概率相同;
②有放回的连续摸![]() 次,则一定摸出
次,则一定摸出![]() 号球两次;
号球两次;
③有放回的连续摸![]() 次,则摸出四个球标号数字之和可能是
次,则摸出四个球标号数字之和可能是![]() .
.
其中正确的序号是
(2)若从袋中不放回地摸两次,求两球标号数字是一奇一偶的概率,(用列表法或树状图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=72°.

(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
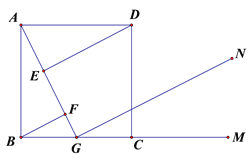
【题目】如图,正方形ABCD中,G是BC中点,DE⊥AG于E,BF⊥AG于F,GN∥DE,M是BC延长线上一点。
(1)求证:△ABF≌△DAE
(2)尺规作图:作∠DCM的平分线,交GN于点H(保留作图痕迹,不写作法和证明),试证明GH=AG。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将笔记本电脑放置在水平桌面上,显示屏OB与底板OA夹角为115°(如图1),侧面示意图为图2;使用时为了散热,在底板下面垫入散热架O′AC后,电脑转到AO′B′的位置(如图3),侧面示意图为图4,已知OA=0B=20cm,B′O′⊥OA,垂足为C.
(1)求点O′的高度O′C;(精确到0.1cm)
(2)显示屏的顶部B′比原来升高了多少?(精确到0.1cm)
(3)如图4,要使显示屏O′B′与原来的位置OB平行,显示屏O′B′应绕点O′按顺时针方向旋转多少度?
参考数据:(sin65°=0.906,cos65°=0.423,tan65°=2.146.cot65°=0.446)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
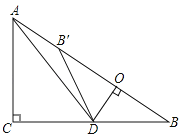
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com