
 如图,一次函数y=kx-2的图象与反比例函数的图象交于A、B两点,过A作AC⊥x轴于点C,己知cos∠AOC=$\frac{2\sqrt{5}}{5}$,OA=$\sqrt{5}$
如图,一次函数y=kx-2的图象与反比例函数的图象交于A、B两点,过A作AC⊥x轴于点C,己知cos∠AOC=$\frac{2\sqrt{5}}{5}$,OA=$\sqrt{5}$分析 (1)通过解直角三角形求出线段AC、OC的长度,从而得出点A的坐标,结合反比例函数图象上点坐标的特点,可得出反比例函数解析式;由点A的坐标利用待定系数法即可求出直线AB的解析式;
(2)根据直线AB的解析式找出直线AB与x轴的交点坐标,再将一次函数解析式代入到反比例函数解析式中,解方程得出点B的坐标,分解三角形AOB,利用三角形的面积公式以及A、B点的坐标即可得出结论;
(3)结合两函数图象,找出反比例函数图象在一次函数图象上方时的x的取值范围即可.
解答 解:(1)在Rt△OCA中,∠OCA=90°,cos∠AOC=$\frac{2\sqrt{5}}{5}$,OA=$\sqrt{5}$,
∴sin∠AOC=$\sqrt{1-co{s}^{2}∠AOC}$=$\frac{\sqrt{5}}{5}$,AC=OA•sin∠AOC=$\sqrt{5}$×$\frac{\sqrt{5}}{5}$=1,OC=OA•cos∠AOC=$\sqrt{5}$×$\frac{2\sqrt{5}}{5}$=2,
∴点A的坐标为(-2,1).
∴k=-2×1=-2,
∴反比例函数的解析式为y=-$\frac{2}{x}$.
将点A(-2,1)代入到y=kx-1中,
1=-2k-2,解得:k=-$\frac{3}{2}$.
∴直线AB的解析式为y=-$\frac{3}{2}$x-2.
(2)令一次函数y=-$\frac{3}{2}$x-2=0,
解得:x=-$\frac{4}{3}$.
将y=-$\frac{3}{2}$x-2代入到反比例函数y=-$\frac{2}{x}$中,
-$\frac{3}{2}$x-2=-$\frac{2}{x}$,即3x2+4x-4=0,
解得:x1=-2,x2=$\frac{2}{3}$.
当x=$\frac{2}{3}$时,y=-$\frac{2}{\frac{2}{3}}$=-3.
∴点B的坐标为($\frac{2}{3}$,-3).
S△AOB=$\frac{1}{2}$×$\frac{4}{3}$×[1-(-3)]=$\frac{8}{3}$.
(3)结合两函数图象可知:
当-$\frac{2}{x}$>-$\frac{3}{2}$x-2时,-2<x<0或x>$\frac{2}{3}$.
故反比例函数值大于一次函数值的自变量取值范围为-2<x<0或x>$\frac{2}{3}$.
点评 本题考查了反比例函数与一次函数的交点问题、三角形的面积公式、待定系数法求函数解析式以及利用函数图象解决不等式,解题的关键是:(1)通过解直角三角形求出点A的坐标;(2)通过解方程求出点B的坐标;(3)利用函数图象解决不等式.本题属于基础题,难度不大,解决该题型题目时,通过解直角三角形求出点的坐标,再利用待定系数法求出函数解析式是关键.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:解答题
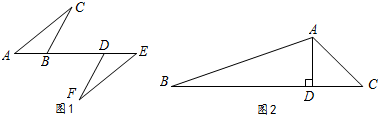
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
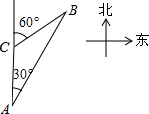
 如图,正比例函数y=-$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$交于M点,已知点M(-4,m),点N为此反比例函数图形上任意一点(不与点M重合),NH垂直于x轴于点H.
如图,正比例函数y=-$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$交于M点,已知点M(-4,m),点N为此反比例函数图形上任意一点(不与点M重合),NH垂直于x轴于点H.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12%+7%=x% | B. | (1+12%)(1+7%)=(1+x%)2 | C. | 12%+7%=2x% | D. | (1+12%)(1+7%)=2(1+x%) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,以AB为直径的⊙O交△ABC的边AC于D、BC于E,过D作⊙O的切线交BC于F,交BA延长线于G,且DF⊥BC.
如图,以AB为直径的⊙O交△ABC的边AC于D、BC于E,过D作⊙O的切线交BC于F,交BA延长线于G,且DF⊥BC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
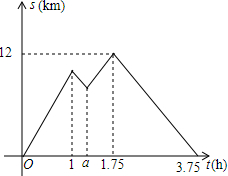
 如图,一艘轮船以40海里/时的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B.轮船继续向北航行2小时后到达C处,发现灯塔B在它的北偏东60°方向.此时轮船与灯塔的距离为( )
如图,一艘轮船以40海里/时的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B.轮船继续向北航行2小时后到达C处,发现灯塔B在它的北偏东60°方向.此时轮船与灯塔的距离为( )| A. | 40海里 | B. | 80海里 | C. | 60海里 | D. | 20海里 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某广场的形状是正方形,可以用64块地砖铺满,设计人员打算用黑、白两种颜色的地砖来铺,并且使上空的一只小鸽子随机地落在广场上时,落在黑色地砖上的概率是$\frac{11}{32}$,请你帮助设计人员设计一种铺设地砖的方案.(把铺褐色地砖的地方涂黑,使设计的图案美观,且是轴对称图形)
如图,某广场的形状是正方形,可以用64块地砖铺满,设计人员打算用黑、白两种颜色的地砖来铺,并且使上空的一只小鸽子随机地落在广场上时,落在黑色地砖上的概率是$\frac{11}{32}$,请你帮助设计人员设计一种铺设地砖的方案.(把铺褐色地砖的地方涂黑,使设计的图案美观,且是轴对称图形)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
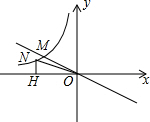
 淆明小长假,李梅陋父母一起去青岛游玩.他们乘坐了一艘可远行12km的船在海上观光,该船远行时顺流匀速行驶.返回时则逆流匀速行驶.远行途中.李梅发现自己携带的游泳圈不知何时落入水中,于是该船立刻原路返回,一刻钟后找到游泳圈,随后继续远行,行驶到离出发地12km远的地方后没有停留又立刻返回.已知游泳圈的漂流速度和水流速度相同,船在远行和返回途中的静水速度相间.船与出发地的距离s(km)与行驶时间t(h)之间的函数图象如图所示.
淆明小长假,李梅陋父母一起去青岛游玩.他们乘坐了一艘可远行12km的船在海上观光,该船远行时顺流匀速行驶.返回时则逆流匀速行驶.远行途中.李梅发现自己携带的游泳圈不知何时落入水中,于是该船立刻原路返回,一刻钟后找到游泳圈,随后继续远行,行驶到离出发地12km远的地方后没有停留又立刻返回.已知游泳圈的漂流速度和水流速度相同,船在远行和返回途中的静水速度相间.船与出发地的距离s(km)与行驶时间t(h)之间的函数图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com