
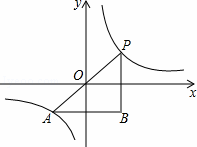
如图,一次函数y=kx+b的图象与反比例函数y=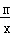 (x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(1)求一次函数、反比例函数的解析式;
(2)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.

解:(1)∵AC=BC,CO⊥AB,A(﹣4,0),
∴O为AB的中点,即OA=OB=4,
∴P(4,2),B(4,0),
将A(﹣4,0)与P(4,2)代入y=kx+b得: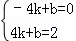 ,
,
解得:k=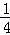 ,b=1,
,b=1,
∴一次函数解析式为y=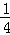 x+1,
x+1,
将P(4,2)代入反比例解析式得:m=8,即反比例解析式为y=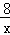 ;
;
(2)假设存在这样的D点,使四边形BCPD为菱形,如图所示,
对于一次函数y=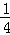 x+1,令x=0,得到y=1,即C(0,1),
x+1,令x=0,得到y=1,即C(0,1),
∴直线BC的斜率为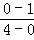 =﹣
=﹣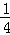 ,
,
设过点P,且与BC平行的直线解析式为y﹣2=﹣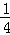 (x﹣4),即y=
(x﹣4),即y=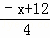 ,
,
与反比例解析式联立得: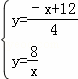 ,
,
消去y得: =
=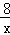 ,
,
整理得:x2﹣12x+32=0,即(x﹣4)(x﹣8)=0,
解得:x=4(舍去)或x=8,
当x=8时,y=1,
∴D(8,1),
此时PD=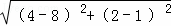 =
=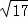 ,BC=
,BC=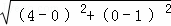 =
=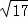 ,即PD=BC,
,即PD=BC,
∵PD∥BC,
∴四边形BCPD为平行四边形,
∵PC=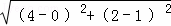 =
=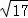 ,即PC=BC,
,即PC=BC,
∴四边形BCPD为菱形,满足题意,
则反比例函数图象上存在点D,使四边形BCPD为菱形,此时D坐标为(8,1).



 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
关于x的反比例函数y=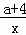 的图象如图,A、P为该图象上的点,且关于原点成中心对称.△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a﹣1)x2﹣x+
的图象如图,A、P为该图象上的点,且关于原点成中心对称.△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a﹣1)x2﹣x+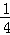 =0的根的情况是 .
=0的根的情况是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )
|
| A. | k> | B. | k≥ | C. | k> | D. | k≥ |
查看答案和解析>>
科目:初中数学 来源: 题型:
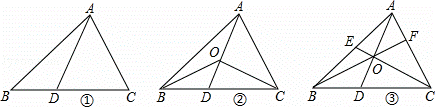
如图,在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.
问题引入:
(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC= ;当点D是BC边上任意一点时,S△ABD:S△ABC= (用图中已有线段表示).
探索研究:
(2)如图②,在△ABC中,O点是线段AD上一点(不与点A、D重合),连结BO、CO,试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比,并说明理由.
拓展应用:
(3)如图③,O是线段AD上一点(不与点A、D重合),连结BO并延长交AC于点F,连结CO并延长交AB于点E,试猜想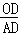 +
+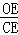 +
+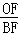 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com