
【题目】如图,在菱形ABCD中,∠BCD=110°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF,则∠CDF等于( )

A. 15° B. 25° C. 45° D. 55°
【答案】A
【解析】
如图,连接BF,根据菱形的性质可得∠CAB=∠CAD=55°,∠ADC=∠ABC=70°,再根据线段垂直平分线的性质可得FB=FA,从而可得∠FBA=∠FAB=55°,根据轴对称性继而可得∠ADF=∠ABF=55°,再根据∠CDF=∠CDA﹣∠ADF即可求得答案.
如图,连接BF,
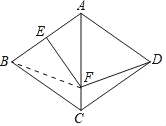
∵四边形是菱形,
∴∠BCD=∠BAD=110°,
∴∠CAB=∠CAD=55°,∠ADC=∠ABC=70°,
∵EF垂直平分线段AB,
∴FB=FA,
∴∠FBA=∠FAB=55°,
∴B、D关于直线AC对称,
∴∠ADF=∠ABF=55°,
∴∠CDF=∠CDA﹣∠ADF=70°﹣55°=15°,
故选A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能判定△ABD≌△BAC的是( )

A. ∠D=∠C B. BD=AC C. ∠CAD=∠DBC D. AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小矩形,且m>n.(以上长度单位:cm)
(1)用含m,n的代数式表示所有裁剪线(图中虚线部分)的长度之和;
(2)观察图形,发现代数式2m2+5mn+2n2可以因式分解为 ;
(3)若每块小矩形的面积为10cm2,四个正方形的面积和为58cm2,试求(m+n)2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC、BD是四边形ABCD的对角线,若E、F、G、H分别是BD、BC、AC、AD的中点,顺次连接E、F、G、H四点,得到四边形EFGH,则下列结论不正确的是( )
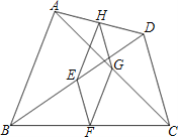
A.四边形EFGH一定是平行四边形B.当AB=CD时,四边形EFGH是菱形
C.当AC⊥BD时,四边形EFGH是矩形D.四边形EFGH可能是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解同学们对垃圾分类知识的知晓程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识.某校环保社团的同学们设计了“垃圾分类知识及投放情况”的问卷,并在本校随机抽取了若干名同学进行了问卷测试,根据测试成绩分布情况,他们将全部成绩分成A,B,C,D四组,并绘制了如下不完整的统计图表:
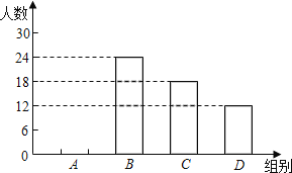
组别 | 分数段 | 频数 | 频率 |
A | 60≤x<70 | a | b |
B | 70≤x<80 | 24 | 0.4 |
C | 80≤x<90 | 18 | c |
D | 90≤x<100 | 12 | 0.2 |
请根据上述统计图表,解答下列问题:
(1)共抽取了多少名学生进行问卷测试?
(2)补全频数分布直方图;
(3)如果测试成绩不低于80分者为“优秀”,请你估计全校2000名学生中,“优秀”等次的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
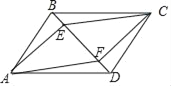
【题目】如图,在ABCD中,经过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.
(1)求证:△AED≌△CFB;
(2)求证:四边形AFCE是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
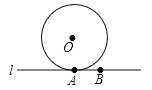
【题目】如图,已知⊙O的半径为5,直线l切⊙O于A,在直线l上取点B,AB=4.
(1)请用无刻度的直尺和圆规,过点B作直线m⊥l,交⊙O于C、D(点D在点C的上方);(保留作图痕迹,不要求写作法)
(2)求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
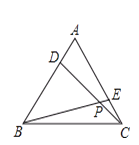
【题目】如图,已知:在等边△ABC中,D、E分别在AB、AC上,且AD=CE,BE、CD相交于点P.
(1)说明△ADC≌△CEB的理由;
(2)求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
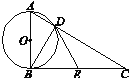
【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O与AC交于点D,E是BC的中点,连接BD,DE.
(1)若![]() ,求sinC;
,求sinC;
(2)求证:DE是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com