
分析 (1)根据根与系数的关系得到AB+AC=2k+3,AB•AC=k2+3k+2,根据勾股定理列出方程,解方程求出k,把k代入原方程检验即可;
(2)①根据三角形的面积公式列出方程,解方程即可;
②分△AQP∽△ABC和△APQ∽△ABC两种情况,根据相似三角形的性质计算即可.
解答 解:(1)由根与系数的关系得:AB+AC=2k+3,AB•AC=k2+3k+2,
∵△ABC是以BC为斜边的直角三角形,
∴AB2+AC2=BC2=52=25
即(2k+3)2-2(k2+3k+2)=25
化简得:k2+3k-10=0
解得 k1=2,k2=-5
当k=2时,方程为x2-7x+12=0,
AB、AC两边为3,4;
当k=-5时,方程为x2+7x+12=0,
AB、AC两边为-3,-4;不合题意,舍去.
综上:当k=2时,△ABC是以BC为斜边的直角三角形;
(2)①∵AB<AC,
∴AB=3,AC=4,
则CP=t,AQ=2t,
由题意得,$\frac{1}{2}$×2t×(4-t)=$\frac{1}{2}×$$\frac{1}{2}$×3×4,
整理得,t2-4t+3=0,
解得,t1=1,t2=3,
答:当t为1或3时,S△APQ=$\frac{1}{2}$S△ABC;
②当$\frac{AQ}{AB}$=$\frac{AP}{AC}$,即$\frac{2t}{3}$=$\frac{4-t}{4}$时,△AQP∽△ABC,
解得t=$\frac{12}{11}$,
当$\frac{AQ}{AC}$=$\frac{AP}{AB}$,即$\frac{2t}{4}$=$\frac{4-t}{3}$时,△APQ∽△ABC,
解得,t=$\frac{8}{5}$,
答:当t=$\frac{12}{11}$或$\frac{8}{5}$时,△APQ 与△ABC相似.
点评 本题考查的是相似三角形的判定和性质、一元二次方程的根与系数的关系,掌握相似三角形的判定定理和性质定理、灵活运用一元二次方程的相关知识是解题的关键.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:选择题
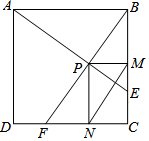 如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,则下列结论:
如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,则下列结论:| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5^2}=5$ | B. | -$\sqrt{3.6}$=-0.6 | C. | $\sqrt{{{(-13)}^2}}=-13$ | D. | $\sqrt{36}=±6$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
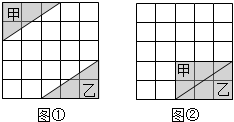 如图,在5×5的方格纸中,将如图①的三角形甲平移到如图②所示的位置,与三角形乙拼成一个长方形.正确的平移方法,可以先将甲向下平移3格,再向右平移2格得到.
如图,在5×5的方格纸中,将如图①的三角形甲平移到如图②所示的位置,与三角形乙拼成一个长方形.正确的平移方法,可以先将甲向下平移3格,再向右平移2格得到.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
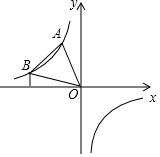 如图,已知A,B两点都在反比例函数y=-$\frac{8}{x}$位于第二象限内的图象上,且△OAB为等边三角形,则△OAB的面积为( )
如图,已知A,B两点都在反比例函数y=-$\frac{8}{x}$位于第二象限内的图象上,且△OAB为等边三角形,则△OAB的面积为( )| A. | 4$\sqrt{3}$cm2 | B. | 6$\sqrt{3}$cm2 | C. | 8$\sqrt{3}$cm2 | D. | 12$\sqrt{3}$cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 男生序号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
| 身高 | 163 | 171 | 173 | 159 | 161 | 174 | 164 | 166 | 169 | 164 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com