
【题目】(1)如图1,图2,图3,在![]() 中,分别以
中,分别以![]() ,
,![]() 为边,向
为边,向![]() 外作正三角形,正四边形,正五边形,
外作正三角形,正四边形,正五边形,![]() ,
,![]() 相交于点O.
相交于点O.
①如图1,求证:![]() ≌
≌![]() ;
;
②探究:如图1,![]() ________;如图2,
________;如图2,![]() _______;如图3,
_______;如图3,![]() _______;
_______;
(2)如图4,已知:![]() ,
,![]() 是以
是以![]() 为边向
为边向![]() 外所作正n边形的一组邻边:
外所作正n边形的一组邻边:![]() ,
,![]() 是以
是以![]() 为边向
为边向![]() 外所作正n边形的一组邻边,
外所作正n边形的一组邻边,![]() ,
,![]() 的延长相交于点O.
的延长相交于点O.
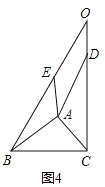
①猜想:如图4,![]() (用含n的式子表示);
(用含n的式子表示);
②根据图4证明你的猜想.

【答案】(1)①见解析;②120°,90°,72°;(2)①![]() ;②见解析.
;②见解析.
【解析】
(1)①要证明△ABE≌△ADC,题中△ABD与△ACE均为等边三角形,容易得出AD=AB,AC=AE,∠DAB=∠EAC=60°,转换可得∠DAC=∠BAE,然后利用SAS证明即可;
②如图1,设AB与CD交于点M,根据①的结论△ABE≌△ADC可得∠ABE=∠ADC,再在△ADM和△BOM中利用三角形的内角和即得∠BOD=∠BAD=60°,进而可求出∠BOC的度数;图2与图3的求解仿图1即可;
(2)欲求∠BOC的度数,可以利用SAS证明△ABE≌△ADC及正n边形的内角和定理,得出∠BOC+∠DAB=180°,进一步即可求得∠BOC的度数.
解:(1)①证明:∵△ABD与△ACE均为等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAE,
∴△ABE≌△ADC(SAS);
②120°,90°,72°.
图1的求解:如图1,设AB与CD交于点M,∵△ABE≌△ADC,∴∠ABE=∠ADC,
∵∠BMO=∠AMD,∴∠BOD=∠BAD=60°,∴∠BOC=120°;
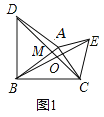
图2与图3的求解仿图1的方法即得.
(2)①![]() .
.
②如图4,依题意,知∠BAD和∠CAE都是正n边形的内角,AB=AD,AE=AC,
∴∠BAD=∠CAE=![]() ,
,
∴∠BAD﹣∠DAE=∠CAE﹣∠DAE,
即∠BAE=∠DAC,
∴△ABE≌△ADC(SAS),
∴∠ABE=∠ADC,
∵∠ADC+∠ODA=180°,
∴∠ABO+∠ODA=180°,
∵∠ABO+∠ODA+∠DAB+∠BOC=360°,
∴∠BOC+∠DAB=180°,
∴∠BOC=180°﹣∠DAB=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,某建筑工程队利用一面墙(墙的长度不限),用40米长的篱笆围成一个长方形的仓库.
(1)求长方形的面积是150平方米,求出长方形两邻边的长;
(2)能否围成面积220平方米的长方形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M.
(1)求∠E的度数.
(2)求证:M是BE的中点.

查看答案和解析>>
科目:初中数学 来源: 题型:
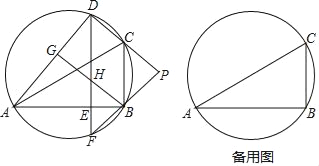
【题目】如图,D是△ABC外接圆上的动点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)求证:BG∥CD;
(2)设△ABC外接圆的圆心为O,若AB=![]() DH,∠OHD=80°,求∠BDE的大小.
DH,∠OHD=80°,求∠BDE的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,点P为∠AOB内一点,OP=8.点M、N分别在OA、OB上.当△PMN周长最小时,下列结论:①∠MPN等于120°;②∠MPN等于100°;③△PMN周长最小值为4;④△PMN周长最小值为8,其中正确的是( )

A.①③B.②③C.①④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,A(0,3)、B(3,0)、C(﹣3,0).

(1)过B作直线MN⊥AB,P为线段OC上的一动点,AP⊥PH交直线M于点H,证明:PA=PH.
(2)在(1)的条件下,若在点A处有一个等腰Rt△APQ绕点A旋转,且AP=PQ,∠APQ=90°,连接BQ,点G为BQ的中点,试猜想线段OG与线段PG的数量关系与位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠A=36°AB的中垂线DE交AC于D,交AB于E,下述结论:(1)BD平分∠ABC;(2)AD=BD=BC;(3)△BCD的周长等于AB+BC;(4)D是AC中点其中正确的命题序号是_________________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com