
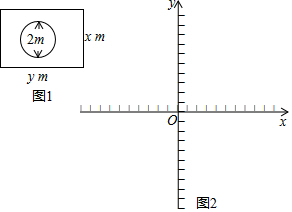
 2016��11��28�գ�����ʮһ�ŷ��زճɹ���½�����緵�ز���½��A��Ϊһ��ֱ��Ϊ2m��Բ�Σ�������Ա�þ����������Χ����1����Ȧ��һ�����Ϊ80m2�ij����Σ��丩����ͼ1��ʾ���賤���εij�Ϊym����Ϊxm��
2016��11��28�գ�����ʮһ�ŷ��زճɹ���½�����緵�ز���½��A��Ϊһ��ֱ��Ϊ2m��Բ�Σ�������Ա�þ����������Χ����1����Ȧ��һ�����Ϊ80m2�ij����Σ��丩����ͼ1��ʾ���賤���εij�Ϊym����Ϊxm������ ��1�����ݾ��ε������ʽ�������������������ɣ�
��2����$\left\{\begin{array}{l}{x+y=18}\\{y=\frac{80}{x}}\end{array}\right.$�����$\left\{\begin{array}{l}{x=10}\\{y=8}\end{array}\right.$��$\left\{\begin{array}{l}{x=8}\\{y=10}\end{array}\right.$�����ʵ�����⣬��֪8��x��4$\sqrt{5}$
��� �⣺��1��������xy=80��
��y=$\frac{80}{x}$��x��0����
����ͼ����ͼ��ʾ��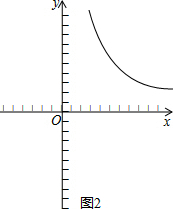
��2����$\left\{\begin{array}{l}{x+y=18}\\{y=\frac{80}{x}}\end{array}\right.$�����$\left\{\begin{array}{l}{x=10}\\{y=8}\end{array}\right.$��$\left\{\begin{array}{l}{x=8}\\{y=10}\end{array}\right.$��
��x=yʱ��x=y=$\sqrt{80}$=4$\sqrt{5}$
����Χ�ɷ���Ҫ��ij����εĿ���ȡֵ��Χ8��x��4$\sqrt{5}$��
���� ���⿼�鷴�������������ʣ�����Ĺؼ������ⷴ���������Ķ��壬���������ѧ֪ʶ������⣮


 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ABCD���ڽ���������AEF����֤��S��EFC=S��ABE+S��ADF��
��ͼ��������ABCD���ڽ���������AEF����֤��S��EFC=S��ABE+S��ADF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 15500��1+x��2=13000 | B�� | 15500��1-x��2=13000 | C�� | 13000��1+x��2=15500 | D�� | 13000��1-x��2=15500 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ������ACBD�У�AB=5��BC=12��AB���д�����BC���ڵ�E����AD����F����BE�ij����ڣ�������
��ͼ������ACBD�У�AB=5��BC=12��AB���д�����BC���ڵ�E����AD����F����BE�ij����ڣ�������| A�� | $\frac{12}{5}$ | B�� | $\frac{13}{5}$ | C�� | $\frac{169}{24}$ | D�� | $\frac{60}{13}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
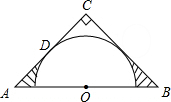 ��ͼ���ڡ�ABC�У���C=90�㣬AC=BC��AB=2����OΪAB���е㣬�Ե�OΪԲ������Բ���AC�����ڵ�D����ͼ����Ӱ���ֵ����Ϊ��������
��ͼ���ڡ�ABC�У���C=90�㣬AC=BC��AB=2����OΪAB���е㣬�Ե�OΪԲ������Բ���AC�����ڵ�D����ͼ����Ӱ���ֵ����Ϊ��������| A�� | 1-$\frac{1}{4}$�� | B�� | $\frac{1}{2}$-$\frac{��}{8}$ | C�� | 2-$\frac{3��}{4}$ | D�� | 2-$\frac{1}{4}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
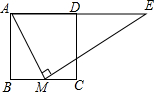 ��ͼ��������ABCD�У�MΪBC��һ�㣬ME��AM��ME��AD���ӳ����ڵ�E����AB=12��BM=5����DE�ij�Ϊ��������
��ͼ��������ABCD�У�MΪBC��һ�㣬ME��AM��ME��AD���ӳ����ڵ�E����AB=12��BM=5����DE�ij�Ϊ��������| A�� | 18 | B�� | $\frac{109}{5}$ | C�� | $\frac{96}{5}$ | D�� | $\frac{25}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
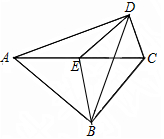 ��ͼ�����ı���ABCD�У���ABC=��ADC=90�㣬EΪ�Խ���AC���е㣬����BE��ED��BD������BAD=58�㣬���EBD�Ķ���Ϊ32�ȣ�
��ͼ�����ı���ABCD�У���ABC=��ADC=90�㣬EΪ�Խ���AC���е㣬����BE��ED��BD������BAD=58�㣬���EBD�Ķ���Ϊ32�ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
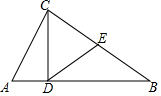 ��ͼ����ABC�У�EΪBC�ߵ��е㣬CD��AB��AB=2��AC=1��DE=$\frac{\sqrt{3}}{2}$�����CDE+��ACD=��������
��ͼ����ABC�У�EΪBC�ߵ��е㣬CD��AB��AB=2��AC=1��DE=$\frac{\sqrt{3}}{2}$�����CDE+��ACD=��������| A�� | 60�� | B�� | 75�� | C�� | 90�� | D�� | 105�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com