
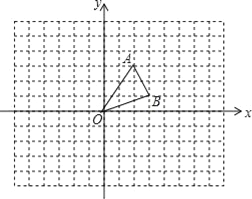
����Ŀ����ƽ��ֱ������ϵ�У���ABO��������������ֱ�Ϊ��A��2��3����B��3��1����O��0��0����
��1������ABO����ƽ��4����λ������ƽ�ƺ�ġ�A1B1O1��
��2������ABO�Ƶ�O˳ʱ����ת180�㣬������ת��õ��ġ�A2B2O����ʱ�ı���ABA2B2����״��������
��3����ƽ�����Ƿ���ڵ�D��ʹ����A��B��O��DΪ������ı�����ƽ���ı��Σ���������ֱ��д���������������е�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��ͼ�μ�������2��ƽ���ı��Σ�3������1��2������1����2������5��4��
��������
��1�����õ�ƽ�Ƶ��������д����A��B��Oƽ�ƺ�Ķ�Ӧ��A1��B1��C1��Ȼ����㼴�ɵõ���A1B1O1��
��2�����ù���ԭ��ԳƵĵ����������д��A2��B2�����꣬���ɵõ���A2B2O�����öԽ�����ƽ�ֵ��ı���Ϊƽ���ı��ο��ж��ı���ABA2B2����״��
��3���������ۣ��ֱ���AB��BO��AOΪ�Խ���ƽ���ı��οɵõ����������ĵ�D��Ȼ��д����Ӧ��D�����꣮
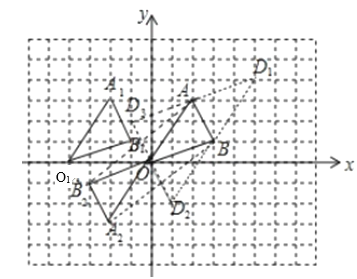
(1)��ͼ,��A1B1O1Ϊ������
(2)��ͼ,��A2B2OΪ����,��ʱ�ı���ABA2B2����״��ƽ���ı���.�ʴ�Ϊƽ���ı��Σ�
(3)����.��ͼ���������ĵ�D������Ϊ(5,4)��(1,2)��(1,2)


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ��Բ���ι��ţ�����ˮ�����ABΪ12m������CDΪ4m.
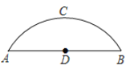
��1�����ŵİ뾶��
��2����һ�ҿ�Ϊ5m�Ļ��������ն���Ϊ�����Σ����߳�ˮ��3.4m����˻����Ƿ���˳��ͨ����Բ���ι��ţ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ��ŷ���dz��Ƴ�۲���������˵����������֪�������������ʣ�����ͨ���۲췢�ֵģ���ʷ�������ң�������ŵĹ۲�һ�����ǽ����ٵ�������ת��Ϊ�Ѿ���Ϥ�Ĺ淶�������ѧ����������һ�־����ձ������Ե���ѧ˼�뷽�������ʽ���Զ���ʽ��������ڶ�λ���ij������м��㣺
![]()
![]()
![]()
![]()
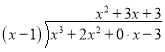
![]()
![]()
![]()
�������Ϸ�������������⣺
��1�����㣺![]() ��
��
��2��������x�Ķ���ʽ![]() �ܱ�����ʽ
�ܱ�����ʽ![]() ��������a��b��Ϊ��Ȼ��������������������a��b��ֵ����Ӧ����.
��������a��b��Ϊ��Ȼ��������������������a��b��ֵ����Ӧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����⣺��1����ͼ�٣���Rt��ABC�У�AB��AC��DΪBC����һ�㣨�����B��C�غϣ������߶�AD�Ƶ�A��ʱ����ת90��õ�AE������EC�����߶�BC��DC��EC֮������ĵ�����ϵʽΪ�� ����
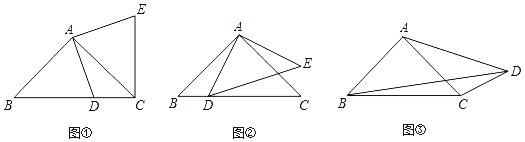
̽������2����ͼ�ڣ���Rt��ABC��Rt��ADE�У�AB��AC��AD��AE������ADE�Ƶ�A��ת��ʹ��D����BC���ϣ���̽���߶�AD��BD��CD֮������ĵ�����ϵ����֤����Ľ��ۣ�
Ӧ�ã���3����ͼ�ۣ����ı���ABCD�У���ABC����ACB����ADC��45�㣮��BD��9��CD��3����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB��AC��P�DZ�BC���е㣬PD��AB��PE��AC������ֱ�ΪD��E
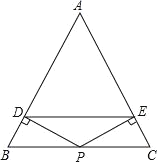
��1����֤��PD��PE��
��2��DE��BCƽ������˵�����ɣ�
��3��������һ��������ʹ�ı���ADPEΪ�����Σ�������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4����E��CD���е㣬AFƽ����BAE��BC�ڵ�F������ADE�Ƶ�A˳ʱ����ת90������ABG����CF�ij�Ϊ____.
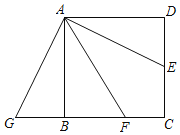
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
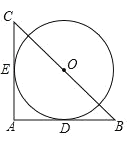
����Ŀ����ͼ���� Rt��ABC ��BC=2![]() ���� BC ���е� O ΪԲ�ĵġ�O �ֱ��� AB��AC ������ D��E ���㣬
���� BC ���е� O ΪԲ�ĵġ�O �ֱ��� AB��AC ������ D��E ���㣬![]() �ij�Ϊ�� ��
�ij��� ��
A.![]() B.
B.![]() C.��D.2��
C.��D.2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����Ӧ����̼��������ɫ�������Ĺ�����С�������������������г�ȥͼ��ݽ���.����ͬʱ�Ӽҳ�����С������150��/�ֵ��ٶ�����һ��ʱ�䣬��Ϣ��5���ӣ�����m��/���ӵ��ٶȵ���ͼ��ݣ�������ʼ����120��/���ӵ��ٶ����У�������ʻ��·��y���ף���ʱ��x�����ӣ��Ĺ�ϵ��ͼ������ͼ����������⣺
��1��ͼ��ݵ�С��ҵľ����� �ף�
��2��a= ��b= ��m= ��
��3��������ʻ��·��y���ף�����ʱ��x�����ӣ��ĺ�������ʽ�� ���������� .

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���Ķ����ϣ�
��֪ʵ��m��n���㣨2m2��n2��1����2m2��n2��1��=80������2m2��n2��ֵ��
�⣺��2m2��n2=t����ԭ���̱�Ϊ��t��1����t��1��=80��������t2��1=80��t2=81������t=��9����Ϊ2m2��n2��0������2m2��n2=9��
�����������ɣ�
�������ַ�����Ϊ���������� ������������ijЩ���ֿ���һ�����壬��������ĸ���棨����Ԫ��������ʹ���ӵ��������
����̽��ʵ����
���������Ķ��������ݣ�����������⣬��д�������̣�
��1����֪ʵ��x��y�����㣨2x2��2y2��3����2x2��2y2��3��=27����x2��y2��ֵ��
��2����֪Rt��ACB������Ϊa��b��c��cΪб�ߣ�������a��b���㣨a2��b2����a2��b2��4��=5����Rt��ACB���Բ�İ뾶��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com