
 如图,在平面直角坐标系中,Rt△PBD的斜边PB落在y轴上,tan∠BPD=$\frac{1}{2}$.延长BD交x轴于点C,过点D作DA⊥x轴,垂足为A,PD与x轴交于点E,OA=8,OB=6.
如图,在平面直角坐标系中,Rt△PBD的斜边PB落在y轴上,tan∠BPD=$\frac{1}{2}$.延长BD交x轴于点C,过点D作DA⊥x轴,垂足为A,PD与x轴交于点E,OA=8,OB=6.分析 (1)求出∠BDP=∠CDP=∠BOC=∠COP=∠DAO=∠DAC=90°,求出∠BPD=∠DCE,推出tan∠DCE=tan∠BPD=$\frac{1}{2}$=$\frac{BO}{OC}$,求出CO=2BO=12即可;
(2)根据tan∠DCE=tan∠BPD=$\frac{1}{2}$=$\frac{DA}{AC}$求出DA=$\frac{1}{2}$AC=2,即可求出D的坐标,代入反比例函数解析式求出k即可.
解答 解:(1)如图: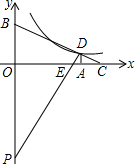
Rt△PBD的斜边PB落在y轴上,
∴BD⊥PD,
又∵DA⊥x轴,OC⊥OB,
∴∠BDP=∠CDP=∠BOC=∠COP=∠DAO=∠DAC=90°,
于是∠BPD+∠OEP=∠DCE+∠DEC=90°,
又∵∠OEP=∠DEC,
∴∠BPD=∠DCE,
∴tan∠DCE=tan∠BPD=$\frac{1}{2}$=$\frac{BO}{OC}$,
∴CO=2BO=12,
C点坐标是(12,0);
(2)∵tan∠DCE=tan∠BPD=$\frac{1}{2}$=$\frac{DA}{AC}$,
∴DA=$\frac{1}{2}$AC=$\frac{1}{2}$(OC-OA)=$\frac{1}{2}$×(12-8)=2,
∴D(8,2),
点D在反比例函数y=$\frac{k}{x}$(k>0)的图象上,
∴k=8×2=16,
∴反比例函数的解析式为 y=$\frac{16}{x}$.
点评 本题考查了用待定系数法求反比例函数的解析式,一次函数和反比例函数的交点问题,解直角三角形的应用,能综合运用知识点进行计算是解此题的关键,难度适中.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com