
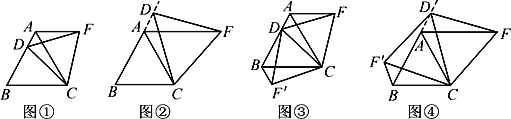
【题目】(1)操作发现:如图①,D是等边△ABC的边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,你能发现AF与BD之间的数量关系吗?并证明你发现的结论;
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与B不重合),连接DC,以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′,连接AF,BF′,探究AF,BF′与AB有何数量关系?并证明你的探究的结论;Ⅱ.如图④,当动点D在等边△ABC的边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
【答案】(1)AF=BD;证明见解析;(2)成立,证明见解析;(3)Ⅰ.AF+BF′=AB;证明见解析;Ⅱ.Ⅰ中的结论不成立.新的结论是AF=AB+BF′;证明见解析.
【解析】解:(1)AF=BD。证明如下:
∵△ABC是等边三角形(已知),∴BC=AC,∠BCA=60°(等边三角形的性质)。
同理知,DC=CF,∠DCF=60°。
∴∠BCA﹣∠DCA=∠DCF﹣DCA,即∠BCD=∠ACF。
在△BCD和△ACF中,∵BC=AC,∠BCD=∠ACF,DC=CF,
∴△BCD≌△ACF(SAS)。∴BD=AF(全等三角形的对应边相等)。
(2)AF=BD仍然成立。
(3)Ⅰ.AF+BF′=AB。证明如下:
由(1)知,△BCD≌△ACF(SAS),则BD=AF。
同理△BCF′≌△ACD(SAS),则BF′=AD。
∴AF+BF′=BD+AD=AB。
Ⅱ.Ⅰ中的结论不成立,新的结论是AF=AB+BF′。证明如下:
在△BCF′和△ACD中,∵BC=AC,∠BC F′=∠ACD,F′C=DC,
∴△BCF′≌△ACD(SAS)。∴BF′=AD(全等三角形的对应边相等)。
又由(2)知,AF=BD,∴AF=BD=AB+AD=AB+BF′,即AF=AB+BF′。
(1)根据等边三角形的三条边、三个内角都相等的性质,利用全等三角形的判定定理SAS可以证得△BCD≌△ACF;然后由全等三角形的对应边相等知AF=BD。
(2)通过证明△BCD≌△ACF,即可证明AF=BD。
(3)Ⅰ.AF+BF′=AB;利用全等三角形△BCD≌△ACF(SAS)的对应边BD=AF;同理△BCF′≌△ACD(SAS),则BF′=AD,所以AF+BF′=AB。
Ⅱ.Ⅰ中的结论不成立,新的结论是AF=AB+BF′:通过证明△BCF′≌△ACD(SAS),则BF′=AD(全等三角形的对应边相等),再结合(2)中的结论即可证得AF=AB+BF′


科目:初中数学 来源: 题型:
【题目】据悉,超级磁力风力发电机可以大幅度提升风力发电效率,但其造价高昂,每座磁力风力发电机,其建造花费估计要6300万美元,“6300万”用科学记数法可表示为( )
A.6.3×103B.6.3×104C.6.3×107D.6.3×108
查看答案和解析>>
科目:初中数学 来源: 题型:
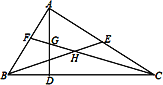
【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
① △ABE的面积与△BCE的面积相等;② ∠AFG=∠AGF;③ ∠FAG=2∠ACF;④ BH=CH
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB、AC引垂线,垂足分别为E、F点.
(1)当点D在BC的什么位置时,DE=DF?并证明.
(2)在满足第一问的条件下,连接AD,此时图中共有几对全等三角形?并请给予写出(不 必证明).
(3)过C点作AB边上的高CG,请问DE、DF、CG的长之间存在怎样的等量关系?并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
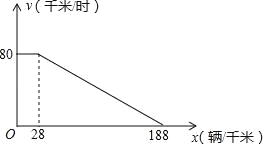
【题目】“城市发展 交通先行”,成都市今年在中心城区启动了缓堵保畅的二环路高架桥快速通道建设工程,建成后将大大提升二环路的通行能力.研究表明,某种情况下,高架桥上的车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的函数,且当0<x≤28时,V=80;当28<x≤188时,V是x的一次函数.函数关系如图所示.
(1)求当28<x≤188时,V关于x的函数表达式;
(2)若车流速度V不低于50千米/时,求当车流密度x为多少时,车流量P(单位:辆/时)达到最大,并求出这一最大值.
(注:车流量是单位时间内通过观测点的车辆数,计算公式为:车流量=车流速度×车流密度)
查看答案和解析>>
科目:初中数学 来源: 题型:
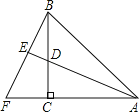
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,BF⊥AD,AD的延长线交BF于E,且E为垂足,则结论①AD=BF,②CF=CD,③AC+CD=AB,④BE=CF,⑤BF=2BE,其中正确的结论的个数是( )
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣3、﹣2、﹣1、4、5中任取两个数相加,若所得的和的最大值是a,最小值是b,则a+b的值是( )
A. ﹣2 B. ﹣3 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com