
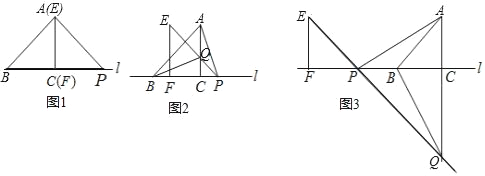
【题目】如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP(备注:当EF=FP,∠EFP=90°时,∠PEF=∠FPE=45°,反之当∠PEF=∠FPE=45°时,当EF=FP).
(1)在图1中,请你通过观察、测量、猜想并写出AB与AP所满足的数量关系和位置关系.
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系和位置关系,并证明你的猜想;
(3)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP、BQ.你认为(2)中所猜想的BQ与AP的结论还成立吗?若成立,给出证明:若不成立,请说明理由.
【答案】(1)AB=AP;AB⊥AP;(2)BQ=AP;BQ⊥AP;证明见解析;(3)成立,证明见解析.
【解析】
(1)根据图形就可以猜想出结论.
(2)要证BQ=AP,可以转化为证明Rt△BCQ≌Rt△ACP;要证明BQ⊥AP,可以证明∠QMA=90°,只要证出∠1=∠2,∠3=∠4,∠1+∠3=90°即可证出.
(3)类比(2)的证明就可以得到,结论仍成立.
(1)AB=AP;AB⊥AP;
∵AC⊥BC且AC=BC,
∴△ABC为等腰直角三角形,
∴∠BAC=∠ABC=![]() (180°﹣∠ACB)=45°,
(180°﹣∠ACB)=45°,
又∵△ABC与△EFP全等,
同理可证∠PEF=45°,
∴∠BAP=45°+45°=90°,
∴AB=AP且AB⊥AP;
(2)BQ=AP;BQ⊥AP.
证明:①由已知,得EF=FP,EF⊥FP,
∴∠EPF=45°.
又∵AC⊥BC,
∴∠CQP=∠CPQ=45°.
∴CQ=CP.
∵在Rt△BCQ和Rt△ACP中,
BC=AC,∠BCQ=∠ACP=90°,CQ=CP,
∴△BCQ≌△ACP(SAS),
∴BQ=AP.
②如图,延长BQ交AP于点M.
∵Rt△BCQ≌Rt△ACP,
∴∠1=∠2.
∵在Rt△BCQ中,∠1+∠3=90°,又∠3=∠4,
∴∠2+∠4=∠1+∠3=90°.
∴∠QMA=90°.
∴BQ⊥AP;
(3)成立.
①如图,∵∠EPF=45°,
∴∠CPQ=45°.
又∵AC⊥BC,
∴∠CQP=∠CPQ=45°.
∴CQ=CP.
∵在Rt△BCQ和Rt△ACP中,
BC=AC,CQ=CP,∠BCQ=∠ACP=90°,
∴Rt△BCQ≌Rt△ACP.
∴BQ=AP.
②如图③,延长QB交AP于点N,则∠PBN=∠CBQ.
∵Rt△BCQ≌Rt△ACP,
∴∠BQC=∠APC.
∵在Rt△BCQ中,∠BQC+∠CBQ=90°,
又∵∠CBQ=∠PBN,
∴∠APC+∠PBN=90°.
∴∠PNB=90°.
∴QB⊥AP.


科目:初中数学 来源: 题型:
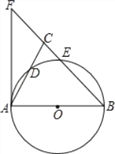
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,延长BC到点F,连接AF,使∠ABC=2∠CAF.
(1)求证:AF是⊙O的切线;
(2)若AC=4,CE:EB=1:3,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在反比例函数y=![]() (x>0)的图像上,点B在反比例函数y=
(x>0)的图像上,点B在反比例函数y=![]() (x>0)的图像上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积是6,则k的值为( )
(x>0)的图像上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积是6,则k的值为( )
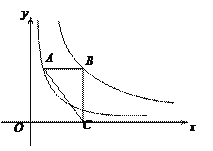
A. 10 B. 12 C. 14 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四位数,记千位上和百位上的数字之和为x,十位上和个位上的数字之和为y,如果x=y,那么称这个四位数为“和平数”.
例如:2635,x=2+6,y=3+5,因为x=y,所以2635是“和平数”.
(1)请判断:3562 (填“是”或“不是”)“和平数”.
(2)直接写出:最小的“和平数”是 ,最大的“和平数”是 ;
(3)如果一个“和平数”的个位上的数字是千位上的数字的两倍,且百位上的数字与十位上的数字之和是14,求满足条件的所有“和平数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。

(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点![]() ,若平移点
,若平移点![]() 到点
到点![]() ,使以点
,使以点![]() 为顶点的四边形是菱形,则正确的平移方法是( )
为顶点的四边形是菱形,则正确的平移方法是( )

A. 向左平移(![]() )个单位,再向上平移1个单位
)个单位,再向上平移1个单位
B. 向左平移![]() 个单位,再向下平移1个单位
个单位,再向下平移1个单位
C. 向右平移![]() 个单位,再向上平移1个单位
个单位,再向上平移1个单位
D. 向右平移2个单位,再向上平移1个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场今年![]() 月的商品销售总额一共是
月的商品销售总额一共是![]() 万元,如图(1)表示的是其中每个月销售总额的情况,图(2)表示的是商场服装部各月销售额占商场当月销售总额的百分比情况,观察图(1)、图(2),下列说法不正确的是( )
万元,如图(1)表示的是其中每个月销售总额的情况,图(2)表示的是商场服装部各月销售额占商场当月销售总额的百分比情况,观察图(1)、图(2),下列说法不正确的是( )
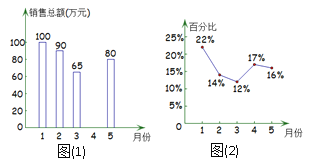
A. 4月份商场的商品销售总额是75万元 B. 1月份商场服装部的销售额是22万元
C. 5月份商场服装部的销售额比4月份减少了 D. 3月份商场服装部的销售额比2月份减少了
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是直角,射线
是直角,射线![]() 在
在![]() 的内部,
的内部,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
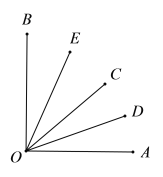
(1)若![]() ,求
,求![]() 的度数.
的度数.
(2)若![]() ,求
,求![]() 的度数.
的度数.
(3)![]() 的度数是否随着射线
的度数是否随着射线![]() 的位置变化而变化?如果不变,请说明理由;如果变化,请说明是如何变化的.
的位置变化而变化?如果不变,请说明理由;如果变化,请说明是如何变化的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:①13+(﹣22)﹣(﹣2)
②﹣4![]()
③(![]() ×(﹣48)
×(﹣48)
④﹣14﹣(![]() ﹣1)[﹣23+(﹣3)2]
﹣1)[﹣23+(﹣3)2]
(2)化简:①(3mn﹣2m2)+(﹣4m2﹣5mn)
②﹣(2a﹣3b)﹣2(﹣a+4b﹣1)
(3)先化简再求值:7x2y﹣2(2x2y﹣3xy2)-(4x2y﹣xy2),其中x=﹣2,y=1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com