解:(1)由题意知:BP=t,CQ=2t,PC=t-2.
∵EC∥AB,∴

∴
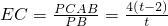
∴

(2)作PF⊥L于F,交DC延长线于M,AN⊥CD于N.则在△PBF中,PF=PB•sin60°=
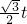
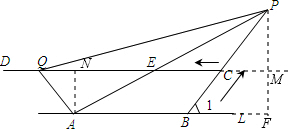
∴S
△APQ=S
△AQE+S
△PQE=

QE•AN+

QE•PM=

QE•PF
=


•
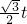
=

(3)此时E为PA的中点,所以C也是PB的中点
则t-2=2,
∴t=4

=

=6(厘米)
分析:(1)根据题意的出BP=t,CQ=2t,PC=t-2.再根据EC∥AB,得出

最后得出EC的值,即可表示出CE和QE的长.
(2)本题关键是得出S与t的函数关系式,那么求面积就要知道底边和高的长,我们可以QE为底边,过P引l的垂线作高,根据P的速度可以用t表示出BP,也就能用BP和∠1的正弦函数求出高,那么关键是求QE的长,我们可以根据Q的速度用时间t表示出CQ,那么只要求出CE即可.因为EC∥BA,那么我们可以用相似三角形的对应线段成比例来求CE的长,根据三角形PEC和PAB相似,可得出关于CE、AB、PC、BC的比例关系式,有BP、BC、AB的值,那么我们就可以用含t的式子表示出CE,也就表示出了QE,那么可根据三角形的面积公式得出关于S与t的函数关系式了.
(3)如果QE恰好平分三角形APQ的面积,那么此时P到CD和CD到l之间的距离就相等,那么C就是PB的中点,可根据BP=2BC求出t的值,然后根据(1)中得出的表示QE的式子,将t代入即可得出QE的值.
点评:本题考查了相似三角形的性质以及解直角三角形的应用等知识点,根据相似三角形得出表示CE的式子是解题的关键所在.



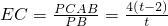

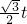

 QE•AN+
QE•AN+ QE•PM=
QE•PM= QE•PF
QE•PF
 •
•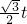 =
=


 最后得出EC的值,即可表示出CE和QE的长.
最后得出EC的值,即可表示出CE和QE的长.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案
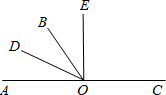 如图所示,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,∠BOE=
如图所示,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,∠BOE= 如图,∠
如图,∠