
【题目】如图,在平面直角坐标系中,直线l1:![]() 分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2:![]() 交于点A.
交于点A.
(1)求出点A的坐标
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.

【答案】(1)A(6,3);(2)y=﹣x+6;(3)存在满足条件的点的P,其坐标为(6,0)或(3,﹣3)或(![]() ,
,![]() +6).
+6).
【解析】(1)把x=0,y=0分别代入直线L1,即可求出y和x的值,即得到B、C的坐标,解由直线BC和直线OA的方程组即可求出A的坐标;(2)设D(x,![]() x),代入面积公式即可求出x,即得到D的坐标,设直线CD的函数表达式是y=kx+b,把C(0,6),D(4,2)代入即可求出直线CD的函数表达式;(3)存在点Q,使以O、C、P、Q为顶点的四边形是菱形,根据菱形的性质能写出Q的坐标.
x),代入面积公式即可求出x,即得到D的坐标,设直线CD的函数表达式是y=kx+b,把C(0,6),D(4,2)代入即可求出直线CD的函数表达式;(3)存在点Q,使以O、C、P、Q为顶点的四边形是菱形,根据菱形的性质能写出Q的坐标.
(1)解方程组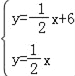 ,得
,得![]() , ∴A(6,3);
, ∴A(6,3);
(2)设D(x, ![]() x),
x),
∵△COD的面积为12,∴![]() ×6×x=12,
×6×x=12,
解得:x=4,∴D(4,2),
设直线CD的函数表达式是y=kx+b,
把C(0,6),D(4,2)代入得:![]() ,解得:
,解得:![]() ,
,
∴直线CD解析式为y=﹣x+6;
(3)在直线l1:y=﹣![]() x+6中,当y=0时,x=12,
x+6中,当y=0时,x=12,
∴C(0,6)
存在点P,使以O、C、P、Q为顶点的四边形是菱形,
如图所示,分三种情况考虑:
(i)当四边形OP1Q1C为菱形时,由∠COP1=90°,得到四边形OP1Q1C为正方形,此时OP1=OC=6,即P1(6,0);
(ii)当四边形OP2CQ2为菱形时,由C坐标为(0,6),得到P2纵坐标为3,
把y=3代入直线直线CQ的解析式y=﹣x+6中,可得3=﹣x+6,解得x=3,此时P2(3,﹣3);
(iii)当四边形OQ3P3C为菱形时,则有OQ3=OC=CP3=P3Q3=6,设P3(x,﹣x+6),
∴x2+(﹣x+6﹣6)2=62,解得x=3![]() 或x=﹣3
或x=﹣3![]() (舍去),此时P3(3
(舍去),此时P3(3![]() ,﹣3
,﹣3![]() +6);
+6);
综上可知存在满足条件的点的P,其坐标为(6,0)或(3,﹣3)或(![]() ,
,![]() +6).
+6).


科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF,并求△DEF的面积;
(2)若连接AD、CF,则这两条线段之间的关系是________________ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,P为Rt△ABC所在平面内任意一点(不在直线AC上),∠ACB=90°,M为AB边中点.操作:以PA、PC为邻边作平行四边形PADC,连结PM并延长到点E,使ME=PM,连结DE.
(1)请你利用图2,选择Rt△ABC内的任意一点P按上述方法操作;

(2)经历(1)之后,观察两图形,猜想线段DE和线段BC之间有怎样的数量和位置关系?请选择其中的一个图形证明你的猜想;
(3)观察两图,你还可得出AC和DE相关的什么结论?请说明理由.
(4)若以A为坐标原点,建立平面直角坐标系,其中A、C、D的坐标分别为(0,0),(5,3),(4,2),能否在平面内找到一点M,使以A、C、D、M为点构造成平行四边形,若不能,说明理由,若能,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知A(0,-2),B(-2,1),C(3,2)
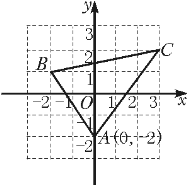
(1)求线段AB、BC、AC的长;
(2)把A、B、C三点的横坐标、纵坐标都乘以2,得到A′、B′、C′的坐标,求A′B′、B′C′、A′C′的长;
(3)以上六条线段成比例吗?
(4)△ABC与△A′B′C′的形状相同吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.
(1)求证:DC是⊙O的切线;
(2)若AB=2,求DC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校七年级学生参加“数学素养水平测试”的成绩情况,在全段学生中抽查一部分学生的成绩,整理后按A、B、C、D四个等级绘制成如下两幅统计图(部分项目不完整).
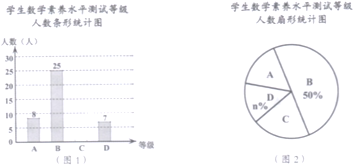
(1)根据统计图所提供的信息,得出抽查学生共有 人,图2中![]() .
.
(2)补全条形统计图1,图2中等级C所对应的扇形的圆心角度数为 .
(3)该校共有800名七年级学生参加素养水平测试,请估算等级A的学生人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图表示一辆汽车在行驶途中的速度v(千米/时)随时间t(分)的变化示意图:
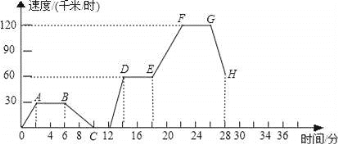
(1)从点A到点B、点E到点F、点G到点H分别表明汽车在什么状态?
(2)分段描述汽车在第0分种到第28分钟的行驶情况;
(3)汽车在点A的速度是多少?在点C呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”,设BC=a,AC﹣b,AB=c.
【特例探索】
(1)如图1,当∠ABE=45°,c=2![]() 时,a= ,b= ;如图2,当∠ABE=30°,c=4时,a= ,b= ;
时,a= ,b= ;如图2,当∠ABE=30°,c=4时,a= ,b= ;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;
【拓展应用】
(3)如图4,在ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2![]() ,AB=3.求AF的长.
,AB=3.求AF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com