
【题目】已知,在矩形ABCD中,AB=a,BC=b,动点M从点A出发沿边AD向点D运动.
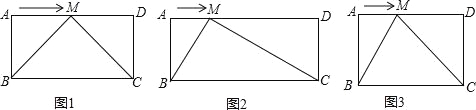
(1)如图1,当b=2a,点M运动到边AD的中点时,请证明∠BMC=90°;
(2)如图2,当b>2a时,点M在运动的过程中,是否存在∠BMC=90°,若存在,请给与证明;若不存在,请说明理由;
(3)如图3,当b<2a时,(2)中的结论是否仍然成立?请说明理由.
【答案】(1)证明见解析(2)存在(3)不成立
【解析】
试题分析:(1)由b=2a,点M是AD的中点,可得AB=AM=MD=DC=a,又由四边形ABCD是矩形,即可求得∠AMB=∠DMC=45°,则可求得∠BMC=90°;
(2)由∠BMC=90°,易证得△ABM∽△DMC,设AM=x,根据相似三角形的对应边成比例,即可得方程:x2﹣bx+a2=0,由b>2a,a>0,b>0,即可判定△>0,即可确定方程有两个不相等的实数根,且两根均大于零,符合题意;
(3)由(2),当b<2a,a>0,b>0,判定方程x2﹣bx+a2=0的根的情况,即可求得答案.
试题解析:(1)∵b=2a,点M是AD的中点,
∴AB=AM=MD=DC=a,
又∵在矩形ABCD中,∠A=∠D=90°,
∴∠AMB=∠DMC=45°,
∴∠BMC=90°.
(2)存在,
理由:若∠BMC=90°,
则∠AMB+∠DMC=90°,
又∵∠AMB+∠ABM=90°,
∴∠ABM=∠DMC,
又∵∠A=∠D=90°,
∴△ABM∽△DMC,
∴![]() ,
,
设AM=x,则![]() ,
,
整理得:x2﹣bx+a2=0,
∵b>2a,a>0,b>0,
∴△=b2﹣4a2>0,
∴方程有两个不相等的实数根,且两根均大于零,符合题意,
∴当b>2a时,存在∠BMC=90°,
(3)不成立.
理由:若∠BMC=90°,
由(2)可知x2﹣bx+a2=0,
∵b<2a,a>0,b>0,
∴△=b2﹣4a2<0,
∴方程没有实数根,
∴当b<2a时,不存在∠BMC=90°,即(2)中的结论不成立.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】现有甲乙两个合唱队,他们的平均身高都是1.70cm,方差分别是S2甲、S2乙,且S2甲>S2乙,则两个队队员的身高较整齐的是_________队(填甲或乙)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】|+2|=________,|-2|=________,-|-2|=________,-|+2|=________,|0|=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y1=![]() x+2的图象分别与坐标轴相交于A,B两点(如图所示),与反比例函数y2=
x+2的图象分别与坐标轴相交于A,B两点(如图所示),与反比例函数y2=![]() (x>0)的图象相交于C点.
(x>0)的图象相交于C点.
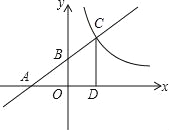
(1)写出A、B两点的坐标;
(2)作CD⊥x轴,垂足为D,如果OB是△ACD的中位线,求反比例函数y=![]() (x>0)的关系式;
(x>0)的关系式;
(3)根据图象(x>0)直接写出y1>y2时的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com