
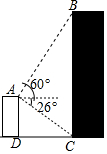
 如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯楼的高度,测得电梯楼顶部B处的仰角为60°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.73,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯楼的高度,测得电梯楼顶部B处的仰角为60°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.73,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49) 分析 首先过点A作AE⊥BC于E,可得四边形ADCE是矩形,即可得CE=AD=15米,然后分别在Rt△ACE中,AE=$\frac{CE}{tan26°}$与在Rt△ABE中,BE=AE•tan60°,即可求得BE的长,继而求得电梯楼的高度.
解答 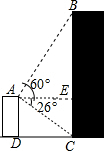 解:过点A作AE⊥BC于E,
解:过点A作AE⊥BC于E,
∵AD⊥CD,BC⊥CD,
∴四边形ADCE是矩形,
∴CE=AD=15米,
在Rt△ACE中,AE=$\frac{CE}{tan26°}$=$\frac{15}{0.49}$≈30.6(米),
在Rt△ABE中,BE=AE•tan60°=52.9(米),
∴BC=CE+BE=15+52.9=67.9(米).
答:电梯楼的高度BC为67.9米.
点评 此题考查了仰角与俯角的知识.此题难度适中,注意能借助仰角或俯角构造直角三角形并解直角三角形是解此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
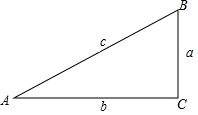 如图,在△ABC中,∠C=90°,定义:斜边与∠A的邻边的比叫做∠A的正割,用“secA”表示,如设该直角三角形各边为a,b,c,则secA=$\frac{c}{b}$,则下列说法正确的是( )
如图,在△ABC中,∠C=90°,定义:斜边与∠A的邻边的比叫做∠A的正割,用“secA”表示,如设该直角三角形各边为a,b,c,则secA=$\frac{c}{b}$,则下列说法正确的是( )| A. | secB•sinA=1 | B. | secB=$\frac{b}{c}$ | C. | secA•cosB=1 | D. | sec2A•sec2B=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 次数 | 2 | 4 | 5 | 8 |
| 人数 | 2 | 2 | 10 | 6 |
| A. | 5 | B. | 5.5 | C. | 6 | D. | 6.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果a=b,那么a-5=b-5 | B. | 如果a=b,那么-$\frac{a}{2}$=-$\frac{b}{2}$ | ||
| C. | 如果a=3,那么a2=3a | D. | 如果$\frac{c}{a}=\frac{c}{b}$,那么a=b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com