
【题目】如图,ABCD的对角线AC、BD相交于点O,AE=CF. 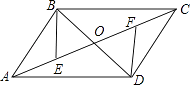
(1)求证:△BOE≌△DOF;
(2)连接DE、BF,若BD⊥EF,试探究四边形EBDF的形状,并对结论给予证明.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴BO=DO,AO=CO,
∵AE=CF,
∴AO﹣AE=CO﹣FO,
∴EO=FO,
在△BOE和△DOF中 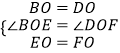 ,
,
∴△BOE≌△DOF(SAS)
(2)证明:四边形EBDF为菱形,等三角形的判定,以及菱形的判定,关键是掌握
理由:∵BO=DO,FO=EO,
∴四边形BEDF是平行四边形,
∵BD⊥EF,
∴四边形EBDF为菱形.
【解析】(1)根据平行四边形的性质可得BO=DO,AO=CO,再利用等式的性质可得EO=FO,然后再利用SAS定理判定△BOE≌△DOF即可;(2)根据BO=DO,FO=EO可得四边形BEDF是平行四边形,再根据对角线互相垂直的平行四边形是菱形可得四边形EBDF为菱形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF. 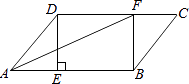
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
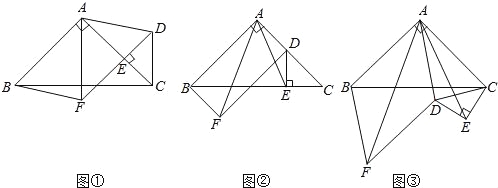
【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系 ;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
(3)在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是用八个全等的直角三角形拼接而成.将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为S1 , S2 , S3 , 若S1+S2+S3=18,则正方形EFGH的面积为( ) 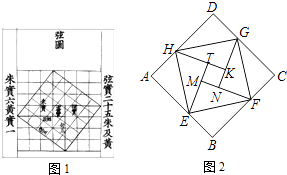
A.9
B.6
C.5
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com