
| ||
| 3 |
| 3 |

| ||
| 3 |
| 3 |
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| ||
| 3 |
| 3 |
| ||
| 3 |
| 1 |
| 2 |
| 42-22 |
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 3 |
3
| ||
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
|
|
| 3 |
| ||
| 2 |
| 3 |
3
| ||
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
(-1-3)2+(10
|
 
练习册系列答案
相关习题
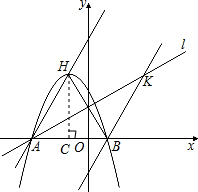
科目:初中数学 来源:不详 题型:解答题 如图,已知抛物线y=x2+bx-3a过点A(1,0),B(0,-3),与x轴交于另一点C. (1)求抛物线的解析式; (2)若在第三象限的抛物线上存在点P,使△PBC为以点B为直角顶点的直角三角形,求点P的坐标; (3)在(2)的条件下,在抛物线上是否存在一点Q,使以P,Q,B,C为顶点的四边形为直角梯形?若存在,请求出点Q的坐标;若不存在,请说明理由.  查看答案和解析>> 科目:初中数学 来源:不详 题型:解答题 如图,己知Rt△OAB的斜边OA在x轴正半轴上,直角顶点B在第一象限,OA=5,OB=
(1)求A、B两点的坐标; (2)求经过O、A、B三点且对称轴平行于y轴的抛物线的解析式,并确定抛物线顶点的坐标. 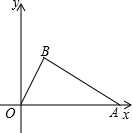 查看答案和解析>> 科目:初中数学 来源:不详 题型:解答题 已知:在平面直角坐标系xOy中,抛物线y=x2+bx+c经过A(1,1)、B(0,4)两点,M为抛物线的顶点. (1)求这条抛物线的表达式及顶点M的坐标; (2)设由(1)求得的抛物线的对称轴为直线l,点A关于直线l的对称点为点C,AC与直线l相交于点D,联结OD、OC.请直接写出C与D两点的坐标,并求∠COM+∠DOM的度数.  查看答案和解析>> 科目:初中数学 来源:不详 题型:单选题 已知函数y=|8-2x-x2|和y=kx+k(k为常数),则不论k为何值,这两个函数的图象( )
查看答案和解析>> 科目:初中数学 来源:不详 题型:解答题 将函数y=
 别与y轴交于O、A两点,与直线x=- 别与y轴交于O、A两点,与直线x=-
(1)求这个新函数的解析式; (2)判断以A、B、C、O四点为顶点的四边形形状,并说明理由; (3)若(2)中的四边形(不包括边界)始终覆盖着二次函数y=x2-2bx+b2+
查看答案和解析>> 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |