
【题目】如图,已知AO为Rt△ABC的角平分线,∠ACB=90°,![]() ,以O为圆心,OC 为半径的圆分别交AO,BC于点D,E,连接ED并延长交AC于点F.
,以O为圆心,OC 为半径的圆分别交AO,BC于点D,E,连接ED并延长交AC于点F.
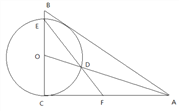
(1)求证:AB是⊙O的切线;
(2)求![]() 的值。
的值。
(3)若⊙O的半径为4,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】分析:(1)作垂直,证半径,先根据AAS证明△OGA≌△OCA,可得OC=OG,可知OG为为⊙O的半径,可得结论;(2)设AC=4x,BC=3x,则AB=5x,根据等角的三角函数可得tan∠CAO=tan∠GAO=![]() ;(3)先根据勾股定理求得AO=
;(3)先根据勾股定理求得AO=![]() ,则求得AD=OA-OD=
,则求得AD=OA-OD=![]() .证明△DFA∽△CDA,列比例式DA:AC=AF:AD,代入可得AF的长,代入可得结论.
.证明△DFA∽△CDA,列比例式DA:AC=AF:AD,代入可得AF的长,代入可得结论.
详解:(1)证明:作OG⊥AB于点G.
∵∠ACB=∠OGA=90°,∠GAO=∠CAO,AO=AO,
∴△OGA≌△OCA,
∴OC=OG,
∵OC为⊙O的半径,
∴AB是⊙O的切线;
(2)解:设AC=4x,BC=3x,则AB=5x,
由切线长定理知,AC=AG=4x,故BG=x.
∵tan∠B=OG:BG=AC:BC=4:3,
∴OG=![]() ,
,
∴tan∠CAO=tan∠GAO=![]() =
=![]() =
=![]() ;
;
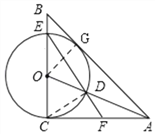
(3)解:由(2)可知 在Rt△OCA中,AO=![]()
∴AD=OA﹣OD=![]()
连接CD,则∠DCF+∠ECD=∠ECD+∠CEF,
∴∠DCF=∠CEF,
又∠CEF=∠EDO=∠FDA,
∴∠DCF=∠ADF,又∠FAD=∠DAC,
∴△DFA∽△CDA,
∴DA:AC=AF:AD,
即![]() :12=AF:
:12=AF:![]()
∴AF=![]() ,CF=12-
,CF=12-![]() =
=![]()
∴![]()


科目:初中数学 来源: 题型:
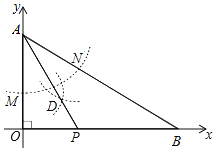
【题目】如图,点A(0,2),在x轴上取一点B,连接AB,以A为圆心,任意长为半径画弧,分别交OA、AB于点M、N,再以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点D,连接AD并延长交x轴于点P.若△OPA与△OAB相似,则点P的坐标为( )
MN的长为半径画弧,两弧交于点D,连接AD并延长交x轴于点P.若△OPA与△OAB相似,则点P的坐标为( )
A. (1,0)B. (![]() ,0)C. (
,0)C. (![]()
![]() ,0)D. (2
,0)D. (2![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
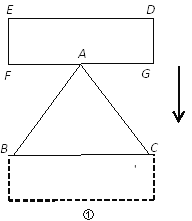
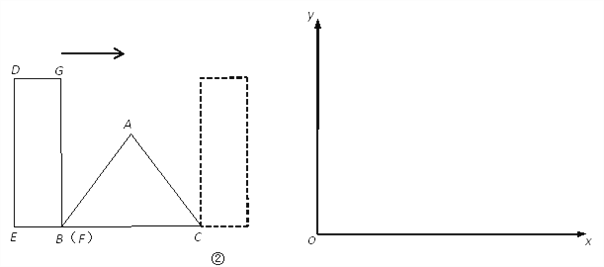
【题目】△ABC中,AB=AC=10,BC=12,矩形DEFG中,EF=4,FG>12.
(1)如图①,点A是FG的中点,FG∥BC,将矩形DEFG向下平移,直到DE与BC重合为止.要研究矩形DEFG与△ABC重叠部分的面积,就要进行分类讨论,你认为如何进行分类,写出你的分类方法(无需求重叠部分的面积).
(2)如图②,点B与F重合,E、B、C在同一直线上,将矩形DEFG向右平移,直到点E与C重合为止.设矩形DEFG与△ABC重叠部分的面积为y,平移的距离为x.
① 求y与x的函数关系式,并写出自变量的取值范围;
② 在给定的平面直角坐标系中画出y与x的大致图象,并在图象上标注出关键点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
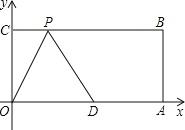
【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为![]() 、
、![]() ,点D是OA的中点,点P在BC边上运动,当
,点D是OA的中点,点P在BC边上运动,当![]() 是等腰三角形时,点Р的坐标为_______________.
是等腰三角形时,点Р的坐标为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
点A、B在数轴上分别表示实数a,b,A,B两点之间的距离表示为|AB|
当A、B两点中有一点在原点时,设点A在原点,如图①|AB|=|OB|=|b|=|a﹣b|
当A、B两点都不在原点时,

(1)如图②,点A,B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
(2)如图③,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|
(3)如图④,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=|a﹣b|
综上所述,数轴上A、B两点之间的距离|AB|=|a﹣b|
请用上面的知识解答下面的问题:
(1)数轴上表示﹣2和﹣4的两点之间的距离是 ,数轴上表示1和﹣3的两点之间的距离是 .
(2)数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2,那么x为 .
(3)当|x+1|+|x﹣2|=5时的整数x的值 .
(4)当|x+1|+|x﹣2|取最小值时,相应的x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,点![]() 把线段
把线段![]() 分割成
分割成![]() ,若以
,若以![]() 为边的三角形是一个直角三角形,则称
为边的三角形是一个直角三角形,则称![]() 是线段
是线段![]() 的勾股点。
的勾股点。
(1)已知点![]() 是线段
是线段![]() 的勾股点,若
的勾股点,若![]() ,求
,求![]() 的长。
的长。
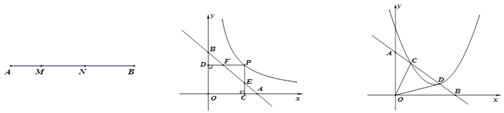
(图1) (图2) (图3)
(2)如图2,点![]() 是反比例函数
是反比例函数![]() 上的动点,直线
上的动点,直线![]() 与坐标轴分别交与
与坐标轴分别交与![]() 两点,过点
两点,过点![]() 分别向
分别向![]() 轴作垂线,垂足为
轴作垂线,垂足为![]() ,且交线段
,且交线段![]() 于
于![]() 。试证明:
。试证明:![]() 是线段
是线段![]() 的勾股点。
的勾股点。
(3)如图3,已知一次函数![]() 与坐标轴交与
与坐标轴交与![]() 两点,与二次函数
两点,与二次函数![]() 交与
交与![]() 两点,若
两点,若![]() 是线段
是线段![]() 的勾股点,求
的勾股点,求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,矩形 OABC 的 顶 点 A(0,3),C(- 1,0). 将 矩 形 OABC 绕原点顺时针旋转 900,得到矩形 OA’B’C’.解答下列问题:
(1)求出直线 BB’的函数解析式;
(2)直线 BB’与 x 轴交于点 M、与 y 轴交于点N,抛物线 y = ax2+ bx + c 的图象经过点C、M、N,求抛物线的函数解析式.
(3)将△MON 沿直线 MN 翻折,点 O 落在点P 处,请你判断点 P 是否在抛物线上,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2 ;
(3)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某演唱会购买门票的方式有两种.
方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元;
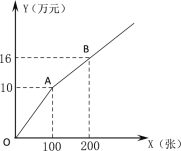
方式二:如图所示.
设购买门票x张,总费用为y万元,方式一中:总费用=广告赞助费+门票费.
(1)求方式一中y与x的函数关系式.
(2)若甲、乙两个单位分别采用方式一、方式二购买本场演唱会门票共400张,且乙单位购买超过100张,两单位共花费27.2万元,求甲、乙两单位各购买门票多少张?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com