
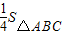 时,判断⊙E与A′C的位置关系,并求相应的tanα值.
时,判断⊙E与A′C的位置关系,并求相应的tanα值.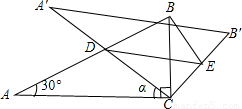
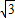 ,由旋转性质求得△ADC∽△BCE,根据比例关系式,求出S与x的函数关系式;
,由旋转性质求得△ADC∽△BCE,根据比例关系式,求出S与x的函数关系式;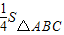 时,求得x的值,判断⊙E和DE的长度大小,确定⊙E与A′C的位置关系,再求tanα值.
时,求得x的值,判断⊙E和DE的长度大小,确定⊙E与A′C的位置关系,再求tanα值.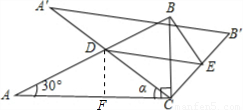 解:(1)∵∠A=a=30°,
解:(1)∵∠A=a=30°,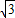 BC=
BC= ,AB=2BC=2.
,AB=2BC=2.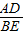 =
= ,
,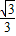 x.
x. ×
×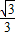 x(2-x)=-
x(2-x)=- x2+
x2+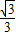 x.(0<x<2)
x.(0<x<2) s△ABC
s△ABC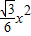 +
+ =
=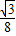 ,
, ,
, .
. 时,BD=2-
时,BD=2- =
= ,BE=
,BE= ×
× =
=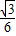 .
.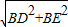 =
= .
. DE=
DE=
 >BE,
>BE,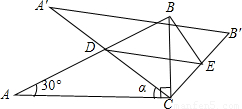 过D作DF⊥AC于F,则
过D作DF⊥AC于F,则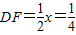 ,
,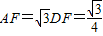 .
. .
.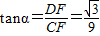 . (12分)
. (12分)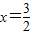 时,
时,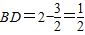 ,
,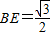 .
.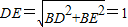 ,
,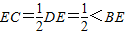 ,
,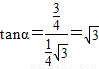 .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2010年全国中考数学试题汇编《二次函数》(08)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2010年福建省龙岩市初中学业质量检查数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《概率》(05)(解析版) 题型:填空题
查看答案和解析>>
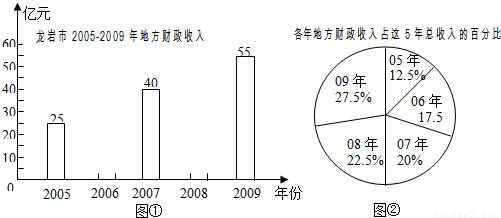
科目:初中数学 来源:2010年全国中考数学试题汇编《数据分析》(06)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《数据分析》(02)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com