
【题目】已知A、B在数轴上对应的数分别用+2、﹣6表示,P是数轴上的一个动点.
![]()
(1)数轴上A、B两点的距离为 .
(2)当P点满足PB=2PA时,求P点表示的数.
(3)将一枚棋子放在数轴上k0点,第一步从k点向右跳2个单位到k1,第二步从k1点向左跳4个单位到k2,第三步从k2点向右跳6个单位到k3,第四步从k3点向左跳8个单位到k4.
①如此跳6步,棋子落在数轴的k6点,若k6表示的数是12,则ko的值是多少?
②若如此跳了1002步,棋子落在数轴上的点k1002,如果k1002所表示的数是1998,那么k0所表示的数是 (请直接写答案).
【答案】(1)8;(2)点P所表示的数为﹣![]() 或10;(3)①18;②3000.
或10;(3)①18;②3000.
【解析】
(1)根据数轴上两点之间距离的计算方法,即两个数差的绝对值,
(2)分两种情况,在点A的左侧和右侧,用(1)中的方法列方程解答即可,
(3)①利用距离公式得到a+2-4+6-8+10-12=12,求出a即可,②同①方法建立方程求出a即可.
(1)|+2﹣(﹣6)|=8,
故答案为:8.
(2)设点表示的数为x,
①当点P在点A的左侧时,有2(2﹣x)=x﹣(﹣6)
解得,x=﹣![]() ,
,
②当点P在点A的右侧时,有x+6=2(x﹣2),
解得,x=10
答:点P所表示的数为﹣![]() 或10.
或10.
(3)①设k0所表示的数为a,由题意得,
a+2﹣4+6﹣8+10﹣12=12,
解得,a=18,
答:k0所表示的数为18.
②由题意得,
a+2﹣4+6﹣8+10﹣12+…+2002﹣2004=1998,
解得,a=3000,
故答案为:3000.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】建设银行的某储蓄员小张在办理业务时,约定存入为正,取出为负. 2019年10月29日,他先后办理了七笔业务: +2000元、-800元、+400元、-800元、+1400元、-1700元、-200元.
(1)若他早上领取备用金4000元,那么下班时应交回银行_________元钱.
(2)请判断在这七次办理业务中,小张在第_______次业务办理后手中现金最多,第_________次业务办理后手中现金最少.
(3)若每办一件业务,银行发给业务量的0.2%作为奖励,小张这天应得奖金多少元?
(4)若记小张第一次办理业务前的现金为0点,用折线统计图表示这7次业务办理中小张手中现金的变化情况.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真阅读材料,并解决下面问题:
(1)以 a 、b 为直角边,以 c 为斜边做四个全等的直角三角形,把这四个直角三角形拼成如图所示形状,使 A 、 E 、 B 三点在一条直线上, B 、 F 、C 三点在一条直线上, C 、G 、D 三点在一条直线上。容易得到:四边形 ABCD 和四边形 EFGH 均是正方形;请用两个不同的代数式 和 表示正方形ABCD 的面积;于是可得到直角三角形关于三边的一个重要的等量关系是 (用含字母 a 、b 、 c 的最简式子填空)
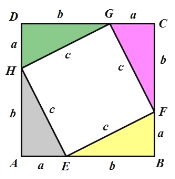
(2)如图,已知正方形 ABCD 中,MAN 45 ,MAN 绕点A 顺时针旋转,它的两边分别交CB 、DC 于点 M 、 N , AH MN 于点 H 。请问: MN 与BM 、 DN 之间有何数量关系?请说明理由;
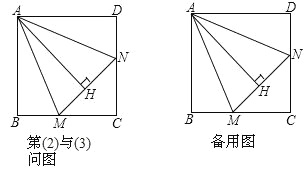
(3)如图,在(2)的情况下,
①请判断 AH 与 AB 之间的数量关系,并说明理由;
②已知 AH 12 ,若 N 还是CD 的中点,结合(1)的结论,求 BM 的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下列各数填在相应的集合里.
﹣![]() ,9,0,+4.3,|﹣0.5|,﹣(+7),18%,(﹣3)4,﹣(﹣2)5,﹣62
,9,0,+4.3,|﹣0.5|,﹣(+7),18%,(﹣3)4,﹣(﹣2)5,﹣62
正有理数集合:{…};
正分数集合:{…};
负整数集合:{…};
自然数集合:{…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)若数轴上两点A、B所表示的数分别为a和b,则有
①A、B两点的中点表示的数为![]() ;
;
②当b>a时,A、B两点间的距离为AB=b﹣a.
(解决问题)数轴上两点A、B所表示的数分别为a和b,且满足|a+2|+(b﹣8)2020=0
(1)求出A、B两点的中点C表示的数;
(2)点D从原点O点出发向右运动,经过2秒后点D到A点的距离是点D到C点距离的2倍,求点D的运动速度是每秒多少个单位长度?
(数学思考)(3)点E以每秒1个单位的速度从原点O出发向右运动,同时,点M从点A出发以每秒7个单位的速度向左运动,点N从点B出发,以每秒10个单位的速度向右运动,P、Q分别为ME、ON的中点.思考:在运动过程中,![]() 的值是否发生变化?请说明理由.
的值是否发生变化?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
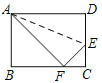
【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处. 已知折痕AE=![]() cm,且tan∠EFC=
cm,且tan∠EFC=![]() ,则矩形ABCD的周长为______cm.
,则矩形ABCD的周长为______cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
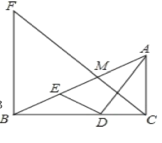
【题目】如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F,BD=4,CD=3.下列结论:①∠AED=∠ADC;②![]() ;③AC
;③AC![]() BE=12;④3BF=4AC;其中正确结论的个数有( )
BE=12;④3BF=4AC;其中正确结论的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com